Chapter 4 Basic exploratory data analysis

4.1 Univariate exploratory analysis

One quantitative variable:

Example: amount in BBBClub data.

Numeric description: Mean, variance, standard deviation, five-point summary (minimum, lower quartile, median, upper quartile, maximum).

##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##      15     127     204     201     273     474

Graphic description: Histogram, box plot.

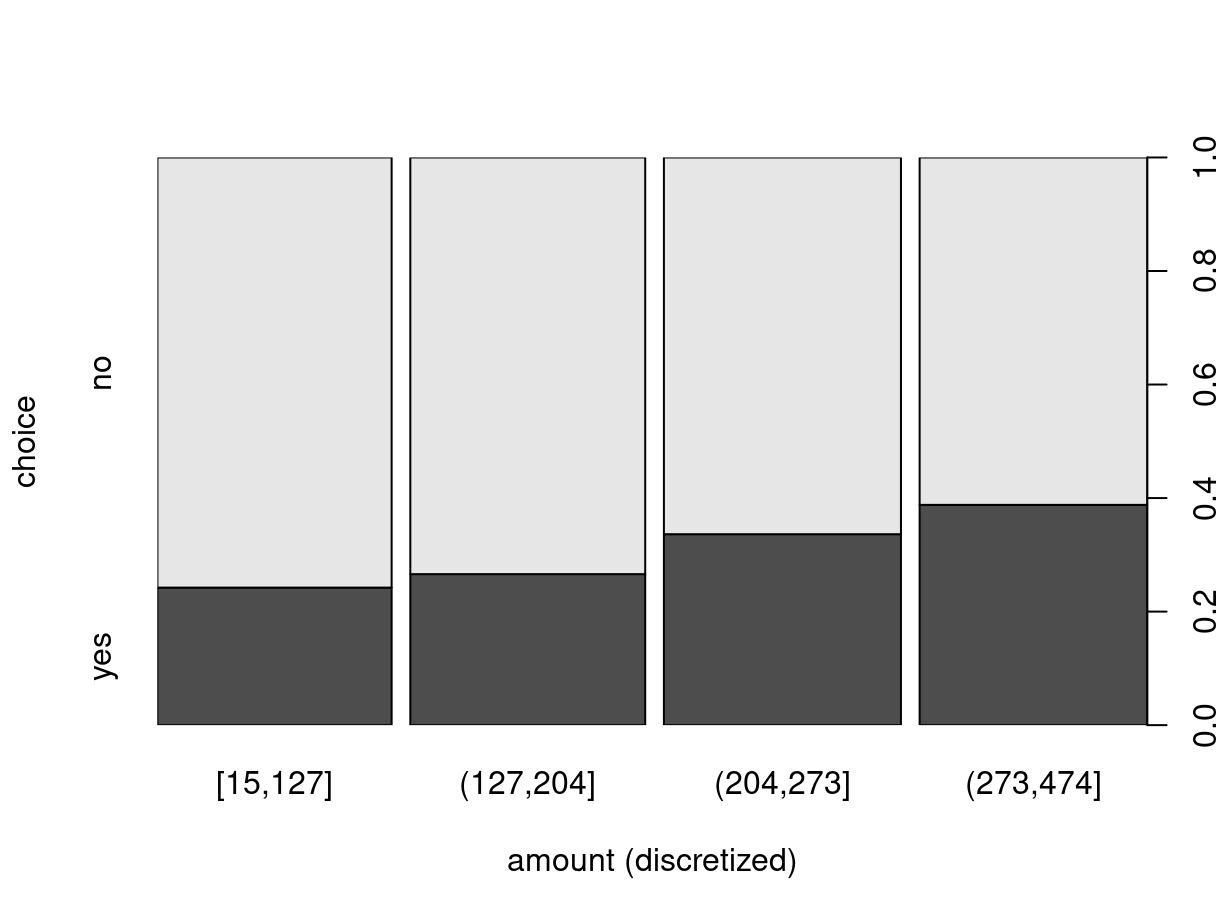
One qualitative variable

Example: gender in BBBClub data.

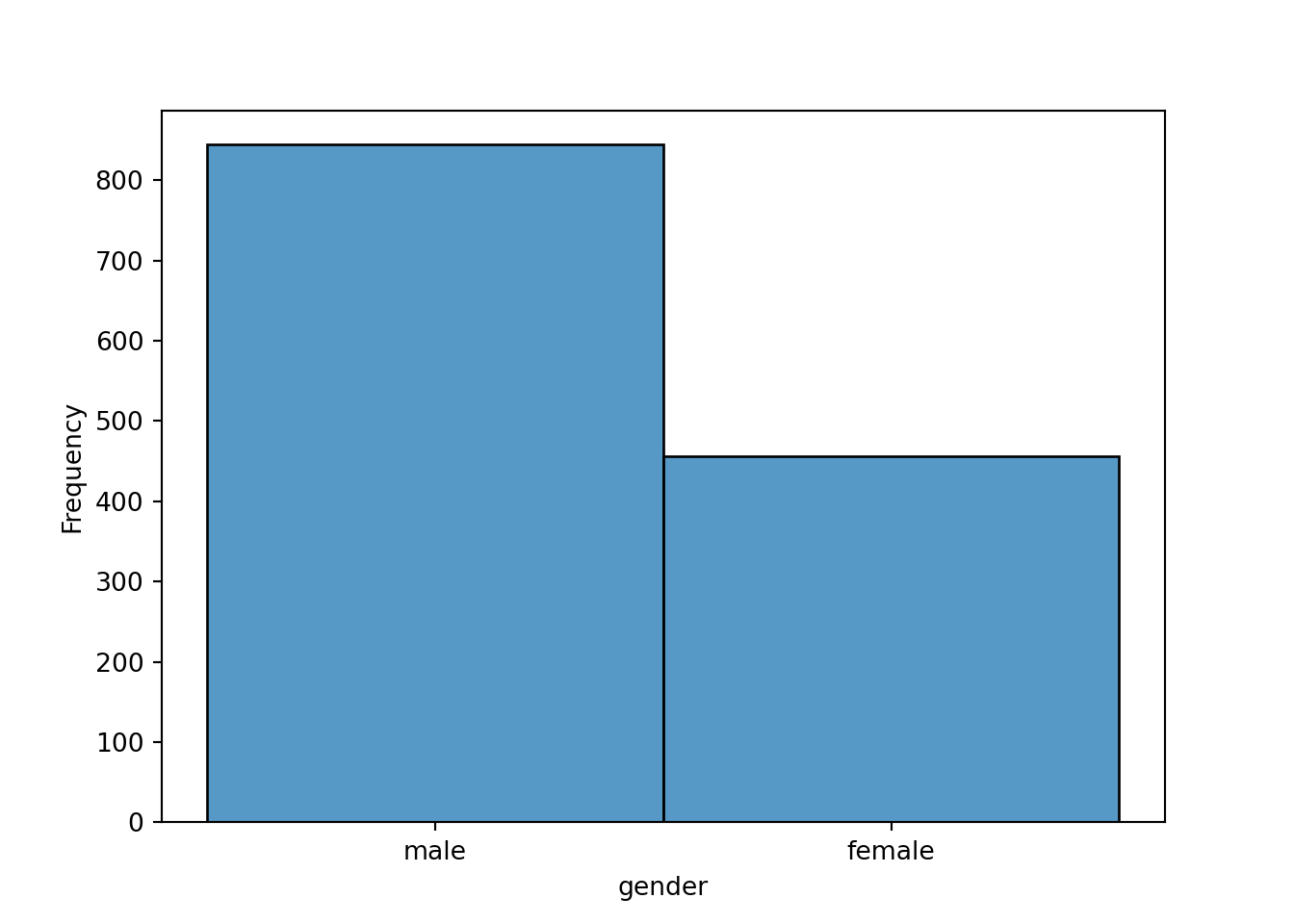
Numeric description: Frequency table (absolute and relative).

## 
## female   male 
##    456    844
## 
## female   male 
##  0.351  0.649

Graphic description: Bar plot.

4.2 Bivariate exploratory analysis

Bivariate exploratory methods depend on the combination of measurement scales of the two variables involved. Moreover, it may be important which variable plays the role of the dependent variable and which is the explanatory variable.

In case there is not natural assignment to dependent/explanatory variable, it is tyically feasible to try both variants.

Dep. vs. expl. Quantitative Qualitative
Quantitative Scatter plot
Correlation		 Box plot
Groupwise statistics
Qualitative Discret. mosaic plot
Discret. contingency table		 Mosaic plot
Contingency table

Two quantitative variables

Example: amount and last.

Numeric description: Correlation coefficient.

Correlation: \(r = 0.452\)

Graphic description: Scatter plot.

One dependent quantitative and one explanatory qualitative variable

Example: amount and gender.

Numeric description: Groupwise statistics.

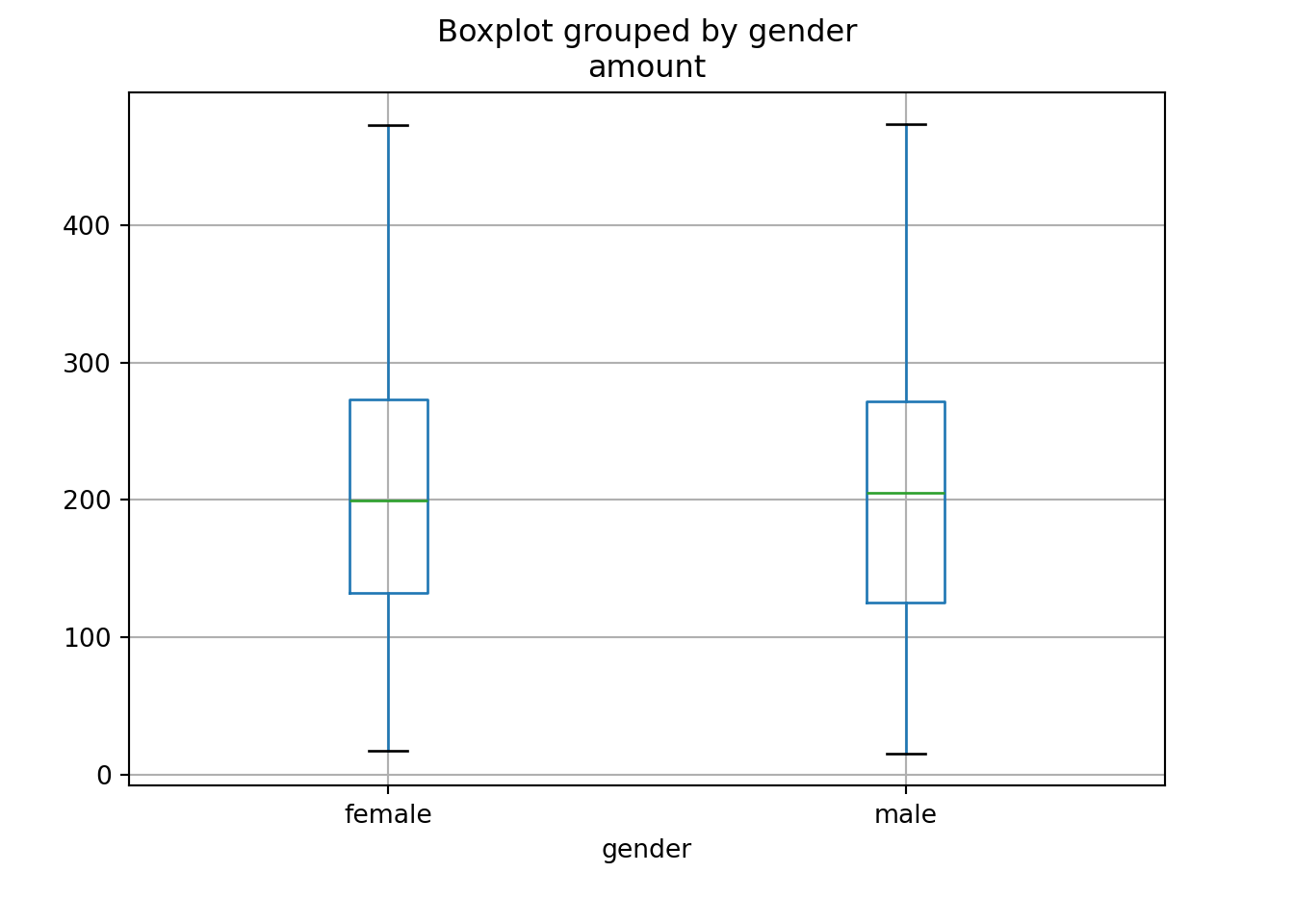
Means: Men \(203.5\), women \(200.2\).

Five-point summary:

Min. \(Q_1\) Median \(Q_3\) Max.
Men 17 132 199.5 273.5 473
Women 15 125 205.5 272.0 474

Graphic description: Parallel box plots.

Two qualitative variables

Example: choice and gender.

Numeric description: Contingency table, odds ratio.

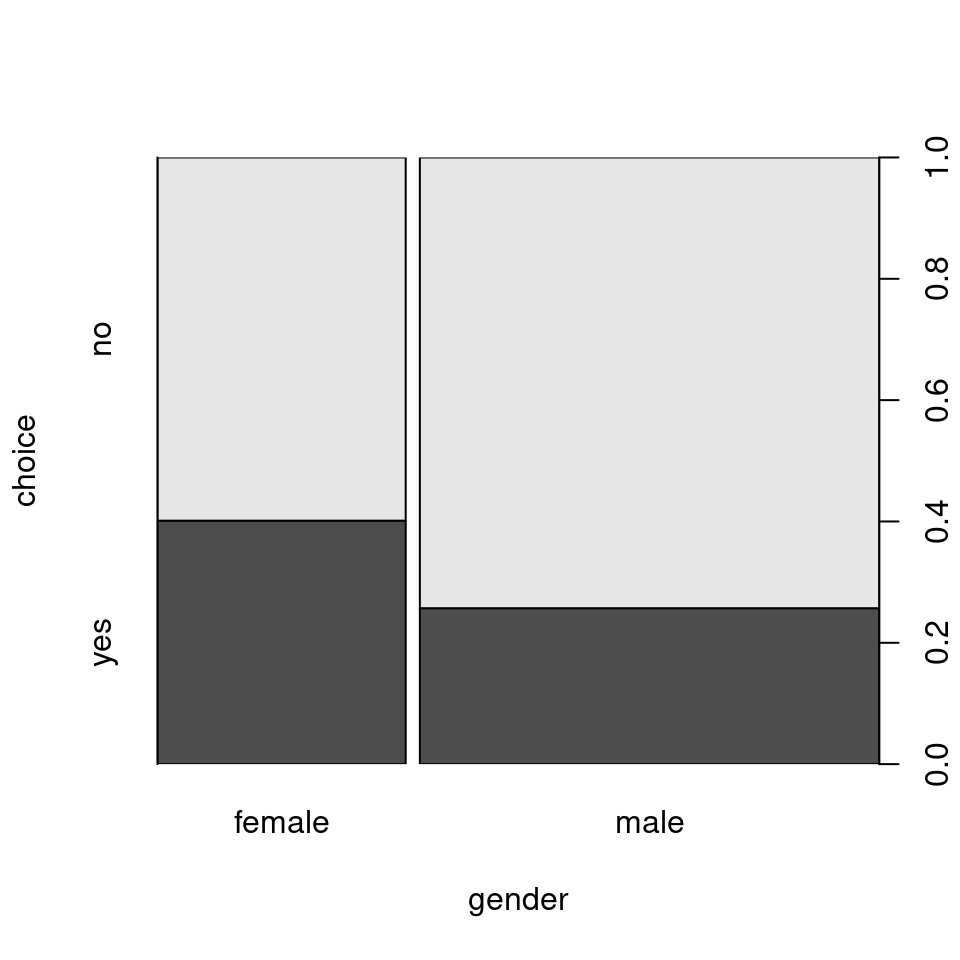
Absolute frequencies with marginal distribution:

Gender vs. choice No Yes Sum
Men 273 183 456
Women 627 217 844
Sum 900 400 1,300

Relative frequencies with marginal distribution:

Gender vs. choice No Yes Sum
Men 0.210 0.141 0.351
Women 0.482 0.167 0.649
Sum 0.692 0.308 1

Conditional relative frequencies:

Gender vs. choice No Yes Sum
Men 0.599 0.401 1
Women 0.743 0.257 1

Graphic description: Mosaic plot.

The mosaic plot is an area-proportional display of a contingency table, i.e., the larger the area of a mosaic tile the larger the corresponding frequency.

Construction: A rectangle is partitioned recursively pertaining to the relative frequencies of the corresponding margin, conditional on all preceding margins.

Here: First split with respect to the relative frequencies of gender. Subsequently split with respect to the conditional relative frequencies of choice given gender.

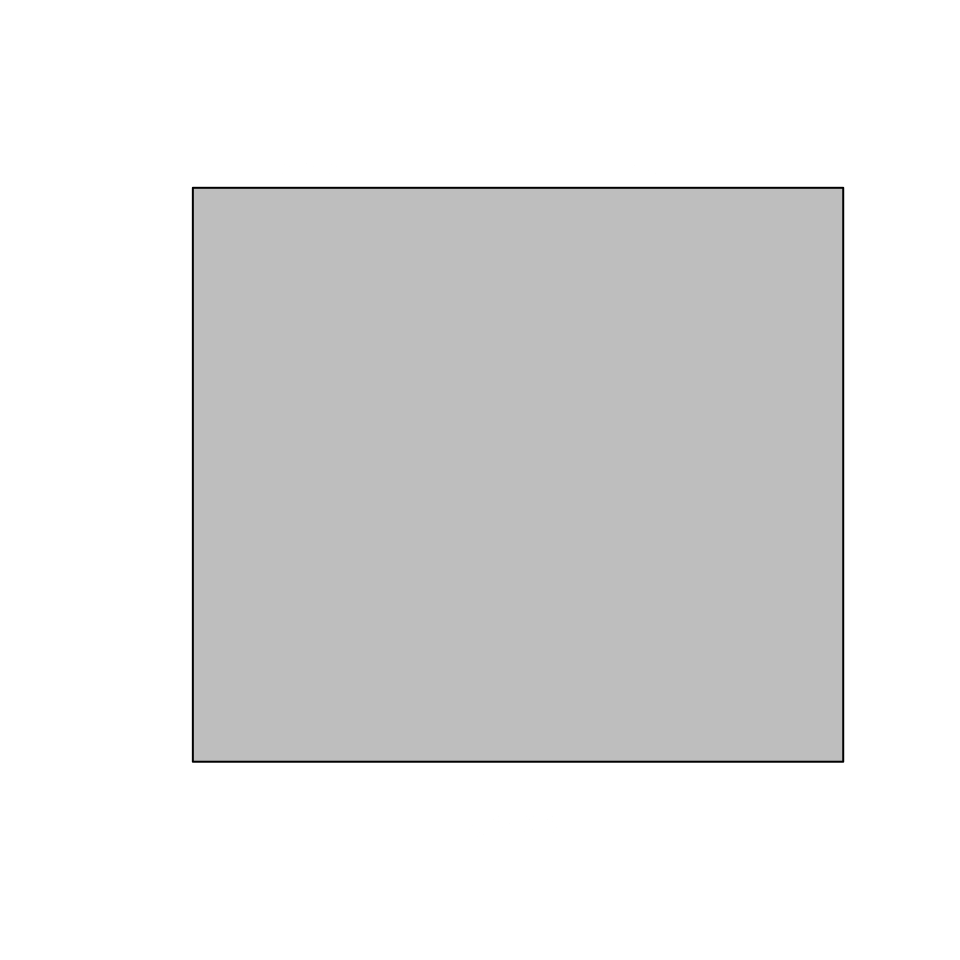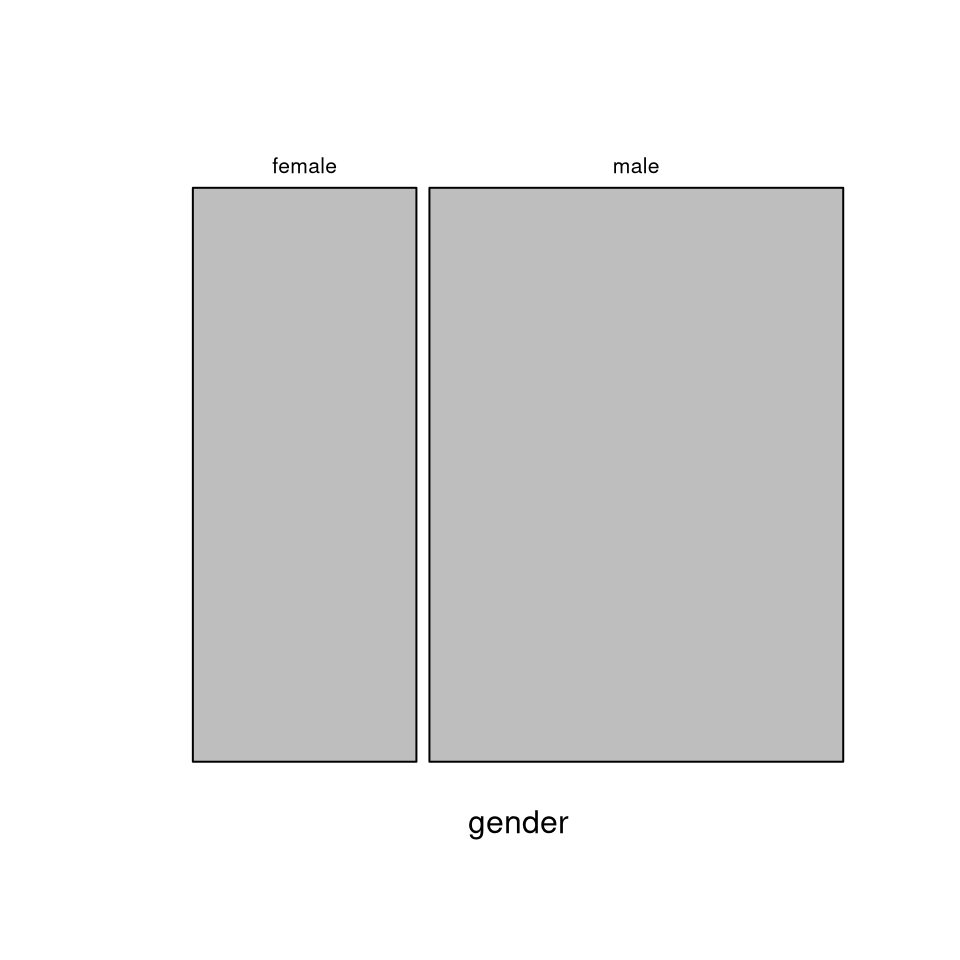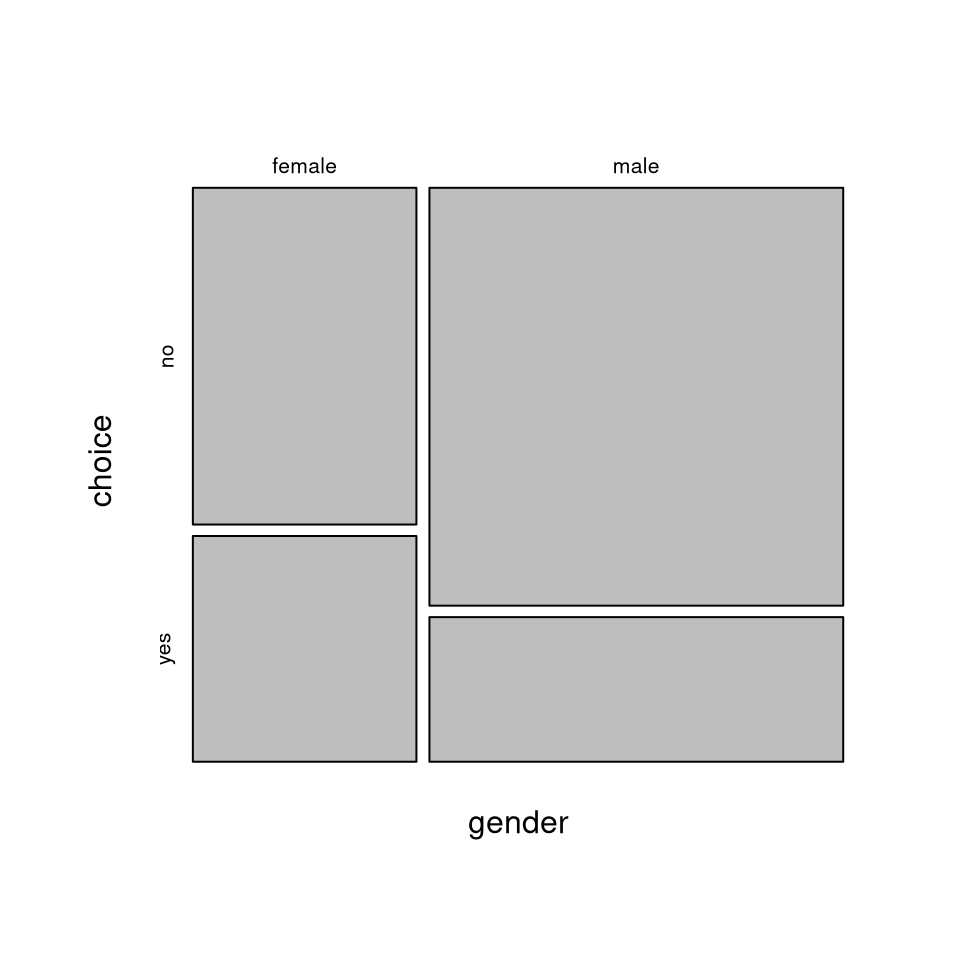
One dependent qualitative and one explanatory quantitative variable

Example: choice and amount.

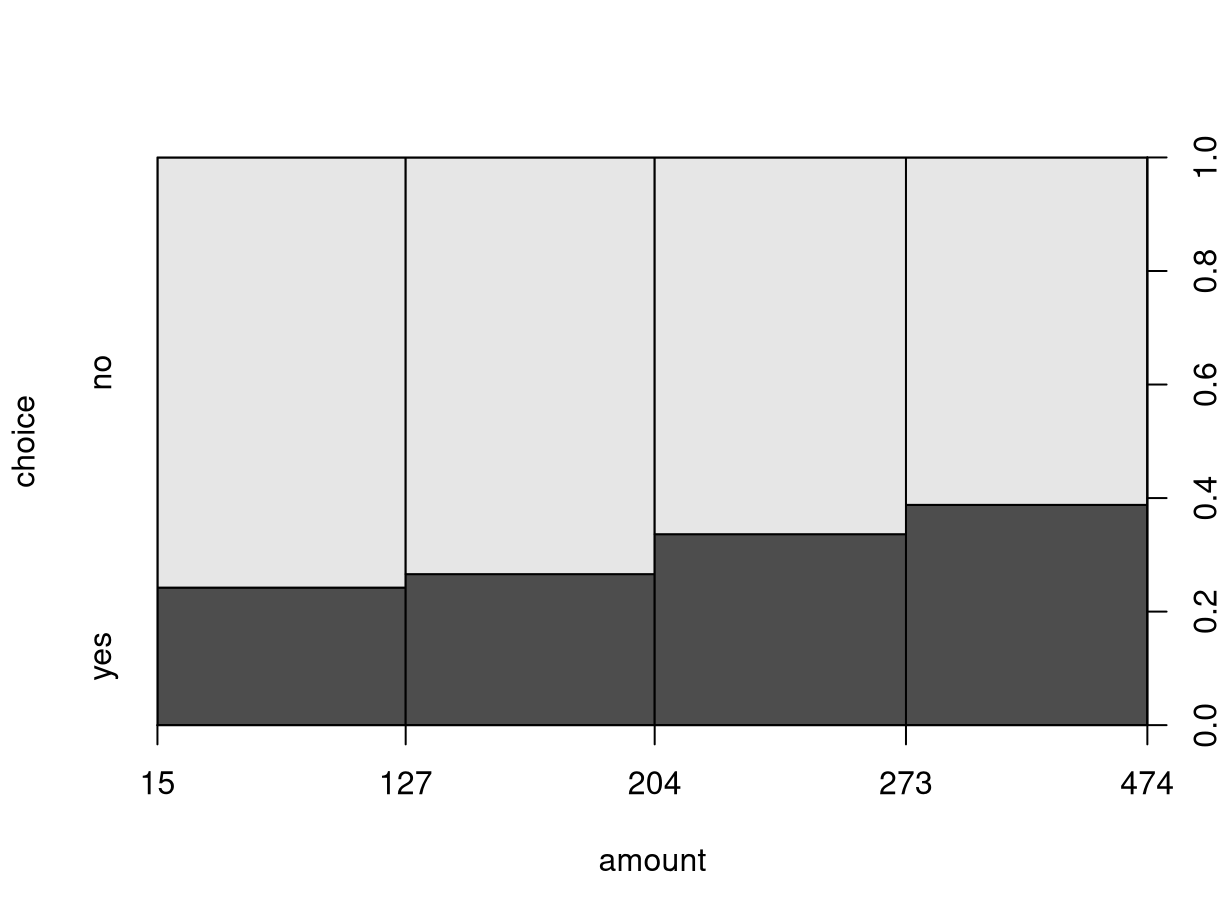
Numeric description: Discretized contingency table.

Graphic description: Discretized mosaic plot.

Idea: Transform the explanatory quantitative variable to a qualitative variable by splitting it into intervals. This is the same idea as used in the histogram.

How to choose the breaks for the intervals? For example based on the five-point summary.

Five-point summary of amount:

Min. \(Q_1\) Median \(Q_3\) Max.
Amount 15 127 204 273 474

Discretized contingency table:

C. vs. A. [15, 127] (127, 204] (204, 273] (273, 474] Sum
No 247 240 219 194 900
Yes 79 87 111 123 400
Sum 326 327 330 317 1,300

4.3 Tutorial

4.3.1 Setup

For illustrating the basics of exploratory data analysis (EDA) we consider the data from the Bookbinders Book Club case study. Download the BBBClub data set as BBBClub.csv or BBBClub.rda.

The readily prepared data frame can be loaded providing 1,300 observations (rows) of 11 variables (columns).

R
load("BBBClub.rda")
Python

For the Python setup, make sure that the required libraries are installed.

# Make sure that the required libraries are installed.
# Import the necessary libraries and classes:
import pandas as pd 
import numpy as np
from matplotlib import pyplot as plt
import seaborn as sns

pd.set_option("display.precision", 4) # Set display precision to 4 digits in pandas and numpy.
# Load dataset
BBBClub = pd.read_csv("BBBClub.csv", index_col=False, header=0)

The dimensions and column names of the data frame are given by:

R
class(BBBClub)
## [1] "data.frame"
dim(BBBClub)
## [1] 1300   11
names(BBBClub)
##  [1] "choice" "gender" "amount" "freq"   "last"   "first"  "child"  "youth"  "cook"  
## [10] "diy"    "art"
Python
print(BBBClub.shape)
## (1300, 11)
print(list(BBBClub.columns))
## ['choice', 'gender', 'amount', 'freq', 'last', 'first', 'child', 'youth', 'cook', 'diy', 'art']
# iterating the columns
for col in BBBClub.columns:
    print(col)
## choice
## gender
## amount
## freq
## last
## first
## child
## youth
## cook
## diy
## art

The variables in the data frame are:

Table 4.1: Variables in the Bookbinder’s Book Club Dataset
Variable Description
choice Did the customer buy the book “The Art History of Florence”?
gender Gender.
amount Total amount spent at BBB Club.
freq Total frequency of purchases at BBB Club.
last Months since last purchase.
first Months since first purchase.
child Number of children’s books purchased.
youth Number of youth books purchased.
cook Number of cooking books purchased.
diy Number of do-it-yourself books purchased.
art Number of art books purchased.

The first few lines of the data frame are given by:

R
head(BBBClub)
##   choice gender amount freq last first child youth cook diy art
## 1    yes   male    113    8    1     8     0     1    0   0   0
## 2    yes   male    418    6   11    66     0     2    3   2   3
## 3    yes   male    336   18    6    32     2     0    1   1   2
## 4    yes   male    180   16    5    42     2     0    0   1   1
## 5    yes female    320    2    3    18     0     0    0   1   2
## 6    yes   male    268    4    1     4     0     0    0   0   0
Python
BBBClub.head()
##   choice  gender  amount  freq  last  first  child  youth  cook  diy  art
## 0    yes    male     113     8     1      8      0      1     0    0    0
## 1    yes    male     418     6    11     66      0      2     3    2    3
## 2    yes    male     336    18     6     32      2      0     1    1    2
## 3    yes    male     180    16     5     42      2      0     0    1    1
## 4    yes  female     320     2     3     18      0      0     0    1    2

Subsequently, we carry out a basic EDA for several of the variables using amount as a typical quantitative and gender as a typical qualitative variable:

R
class(BBBClub$amount)
## [1] "integer"
class(BBBClub$gender)
## [1] "factor"
Python
print(BBBClub['amount'].dtypes) 
## int64
print(BBBClub['gender'].dtypes)
## object

4.3.2 One quantitative variable

For describing a quantitative variable the usual basic summary statistics can be employed: mean, variance, standard deviation, minimum and maximum, and five-point summary (minimum, lower quartile, median, upper quartile, maximum).

R

Corresponding functions are easily available in base R.

Writing mean(BBBClub$amount) with the $ extractor is somewhat tedious in interactive use, we first attach() the BBBClub data frame so that we can write mean(amount) instead. We want to emphasize, though, that attach() should be used with care:

  • Only attach at most one data frame at a time.
  • Do so only for accessing variables in the data frame and not for transforming them.
  • Employ functions with formula interfaces where available (that do not require extraction with $).
  • Detach the data frame again when the exploratory analysis has been completed.
attach(BBBClub)

With the data attached we now compute the following basic statistics:

mean(amount)
## [1] 201.369
var(amount)
## [1] 8954.53
sd(amount)
## [1] 94.6284
min(amount)
## [1] 15
max(amount)
## [1] 474
fivenum(amount)
## [1]  15 127 204 273 474
summary(amount)
##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##      15     127     204     201     273     474

The final summary() is a collection of all other statistics above except for variance and standard deviation. The customers have spent an amount between 15 and 474 dollars with a median and average of 204 and 201.369231, respectively. The central 50% of customers have spent between 127 and 273 dollars.

Note: Many of the functions above return NA (for “not available”) in case any of the individual observations in a vector is NA. In order to ignore these missing values (by removing them first) for computing the statistics, one can then typically set the argument na.rm = TRUE.

Python

Corresponding functions are easily available in pandas.

amount = BBBClub['amount']
print(amount.mean())
## 201.36923076923077
print(amount.var())
## 8954.525611417066
print(amount.std())
## 94.62835521880884
print(amount.min())
## 15
print(amount.max())
## 474
print(amount.describe())
## count    1300.0000
## mean      201.3692
## std        94.6284
## min        15.0000
## 25%       127.0000
## 50%       204.0000
## 75%       273.0000
## max       474.0000
## Name: amount, dtype: float64

We provide the fivenum() function to compute the five-point summary (minimum, lower quartile, median, upper quartile, maximum).

def fivenum(data):
    """
    A function that computes the five-number summary.
    
    :param data: A column of 'pandas.DataFrame'
    :param column: The column of the DataFrame to use (string)
    
    :returns: The five numbers (list)
    """
    five_num = list()
    five_num.append(data.min()) # Min
    five_num.append(data.quantile(q=0.25)) # 1st Quantile
    five_num.append(data.quantile(q=0.5)) # Median
    five_num.append(data.quantile(q=0.75)) # 3st Quantile
    five_num.append(data.max()) # Max
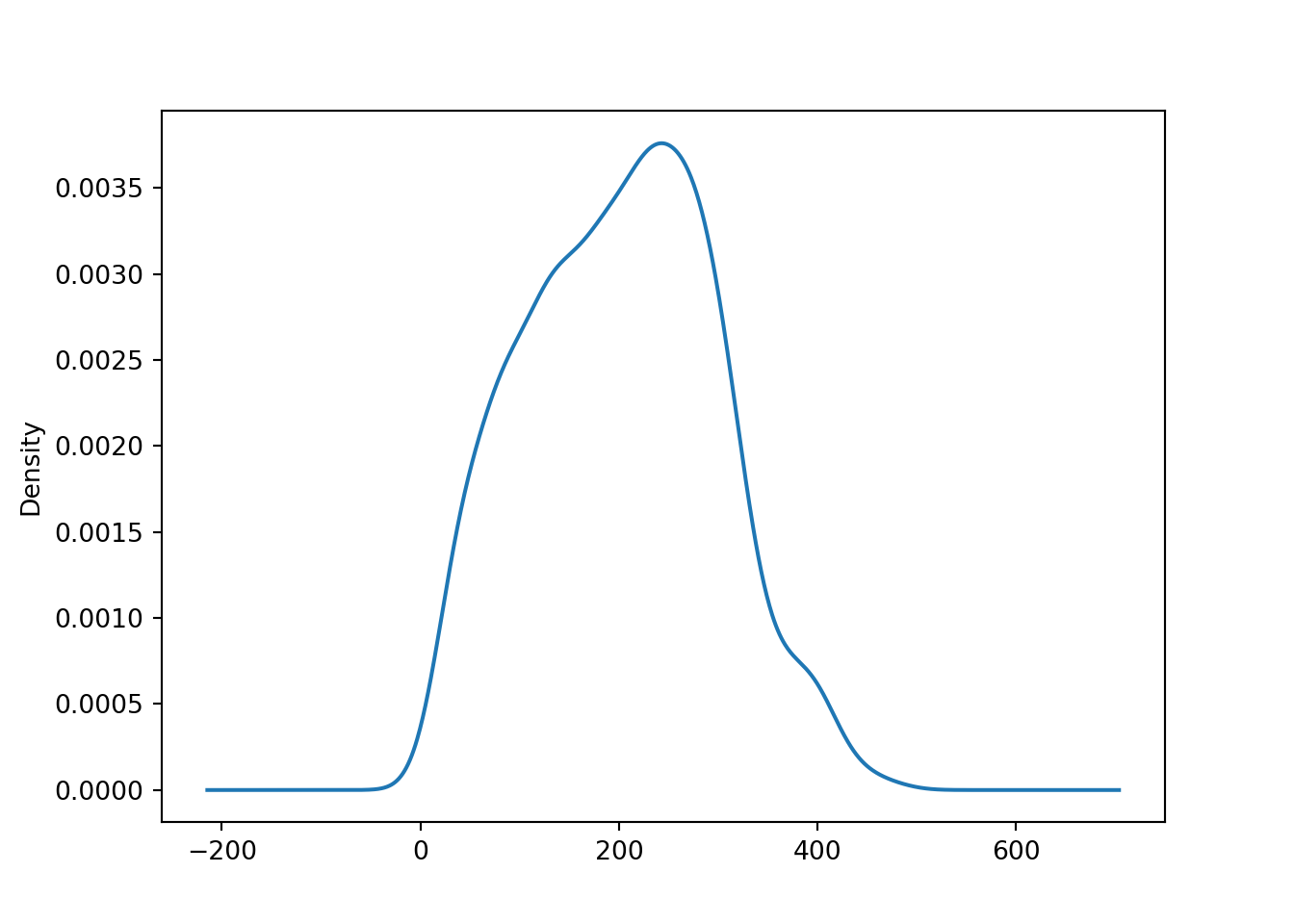
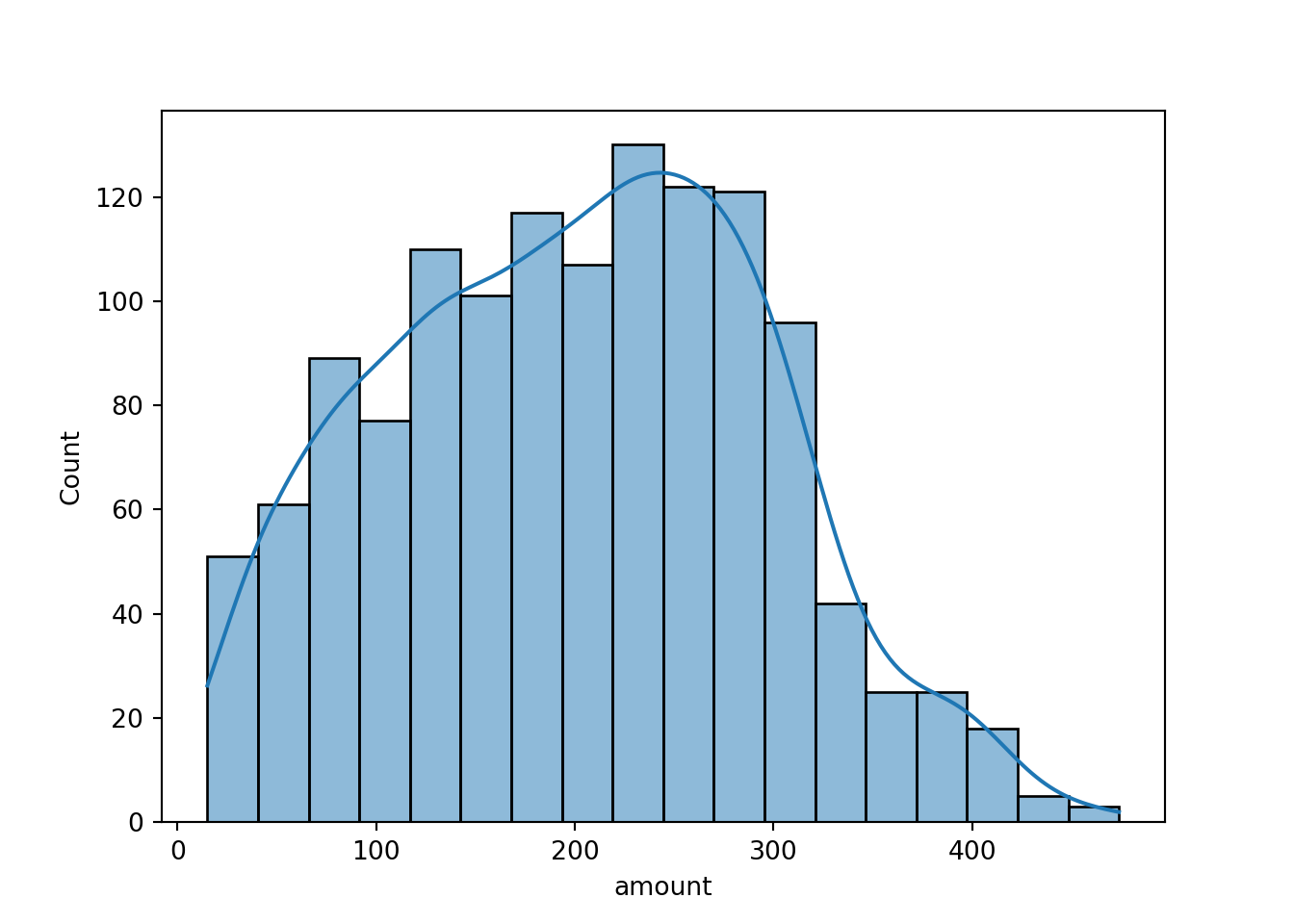
    return five_num
print(fivenum(amount))
## [np.int64(15), np.float64(127.0), np.float64(204.0), np.float64(273.0), np.int64(474)]

Somewhat easier to grasp compared to the numerical summaries are graphical visualizations like the histogram (based on binning the data) or the kernel density (based on smoothing).

R

These can be generated with hist() (that directly plots the histogram by default) and density() (that needs an explicitly plot() call), respectively.

hist(amount)
plot(density(amount))

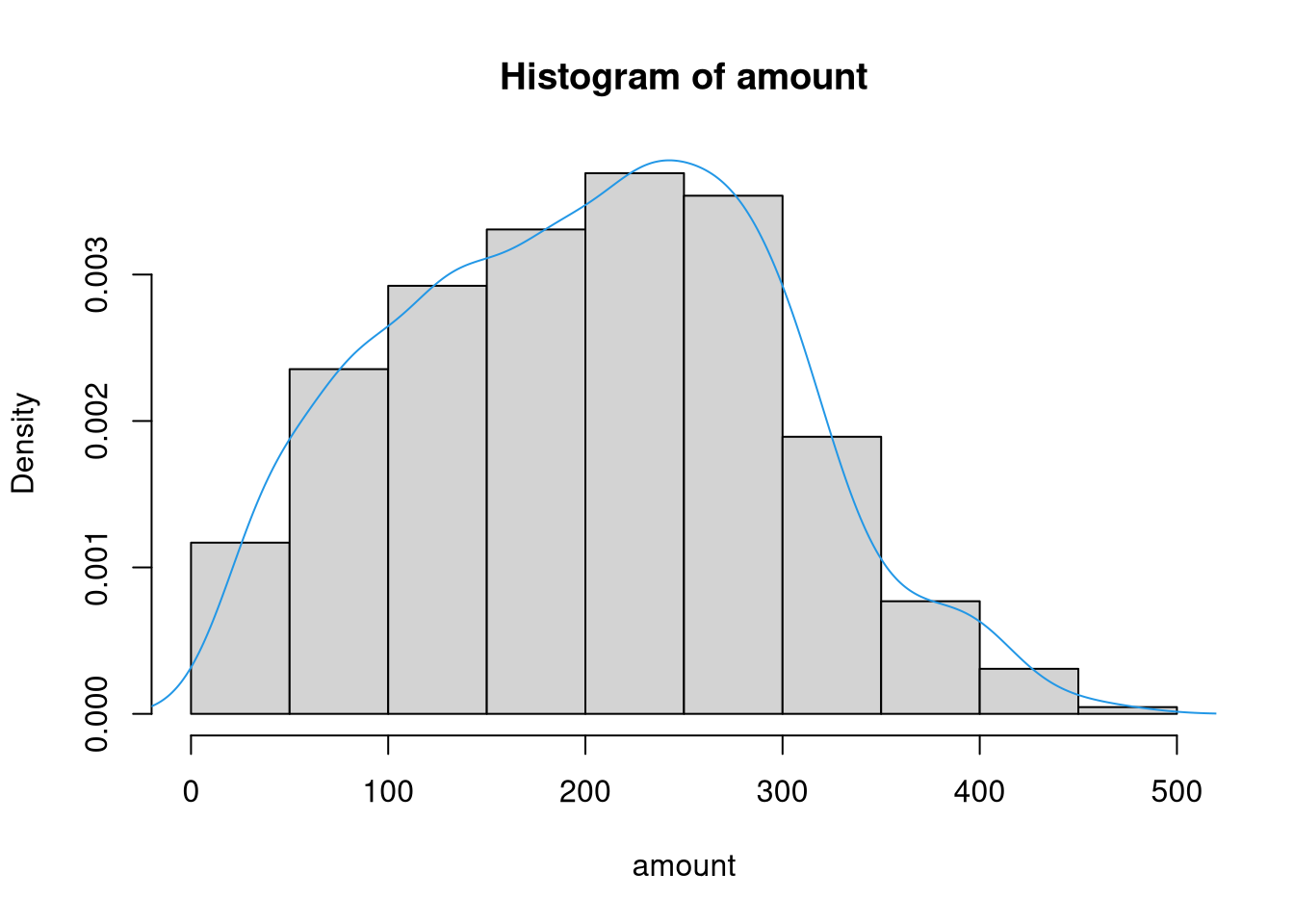
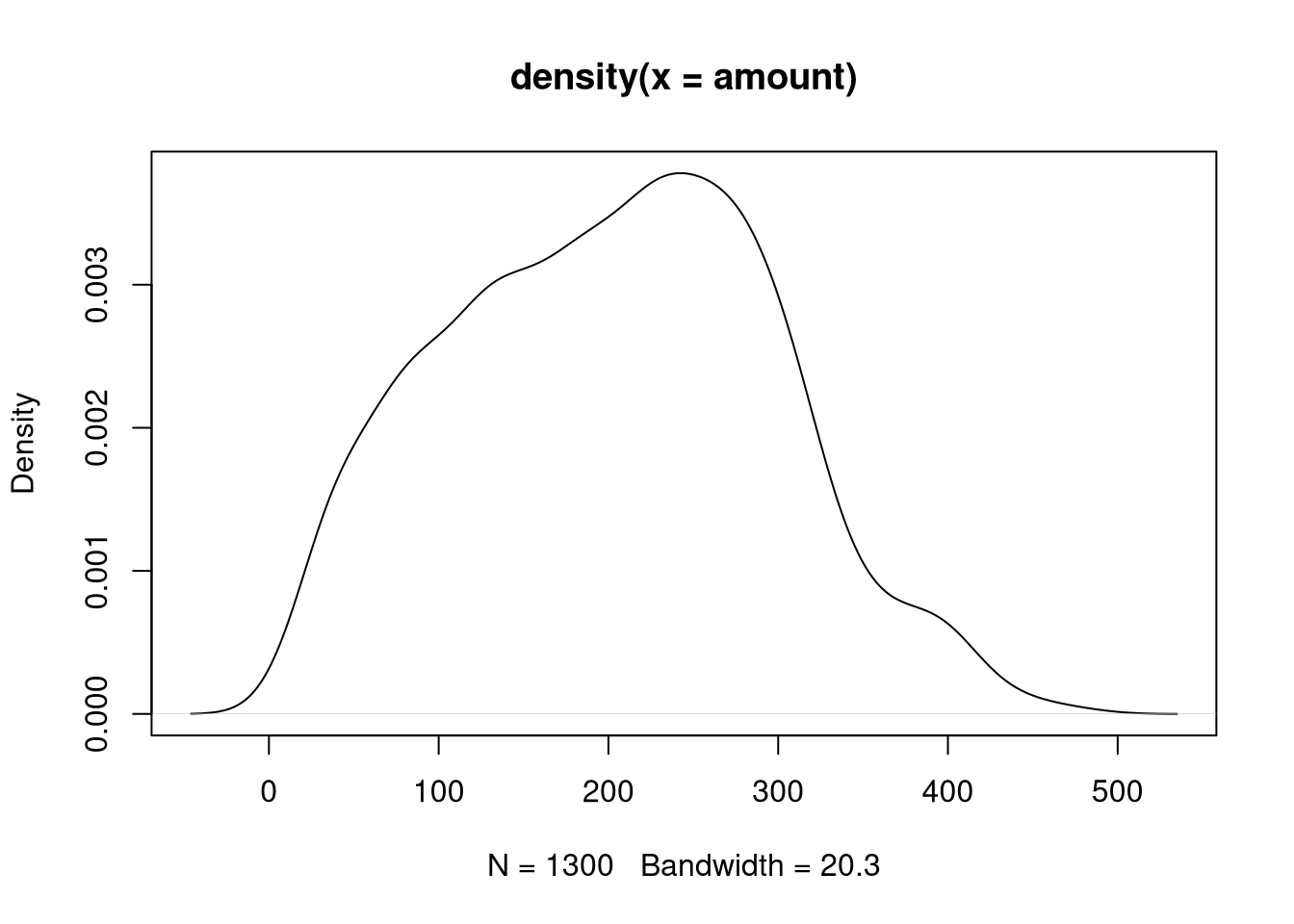
If a density histogram (with overall area 1) is used instead of the default frequency histogram (at least when bins are equidistant), both displays can also easily be combined:

hist(amount, freq = FALSE)
lines(density(amount), col = 4)

Python
amount.hist(grid=False)
plt.show()

amount.plot.kde()
plt.show()

We will use the library seaborn for more advanced plotting.

sns.histplot(data=amount, kde=True)
plt.show()

Both displays show that the amount variable is unimodal and slightly right-skewed.

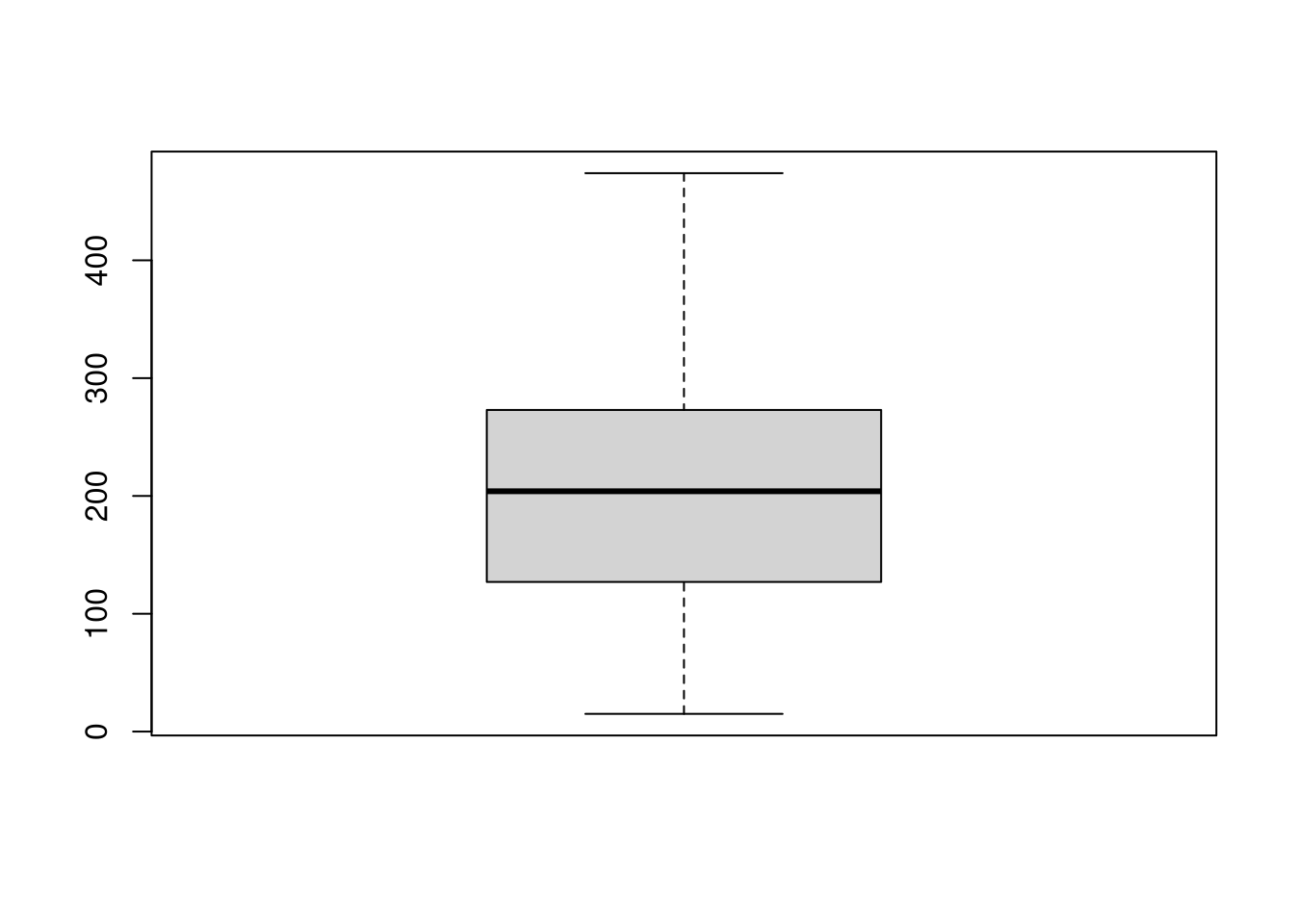
Another graphical display that compresses the data even further is the box plot. While this is probably more appealing for visualizing multiple groups in parallel (see below), it is also possible to generate a box plot for a single variable, essentially showing the five-point summary above:

R
boxplot(amount)

Python
BBBClub.boxplot(column='amount')
# seaborn version: sns.boxplot(y=amount)
plt.show()

In case the quantitative variable is measured discretely with relatively few distinct values, it might make sense to also consider frequency tables in addition to the summary statistics above. To illustrate this we employ the variable last that codes the number of months since the last purchase in the book club. At most this can be 12 because every customer is required to make at least one purchase per year.

R

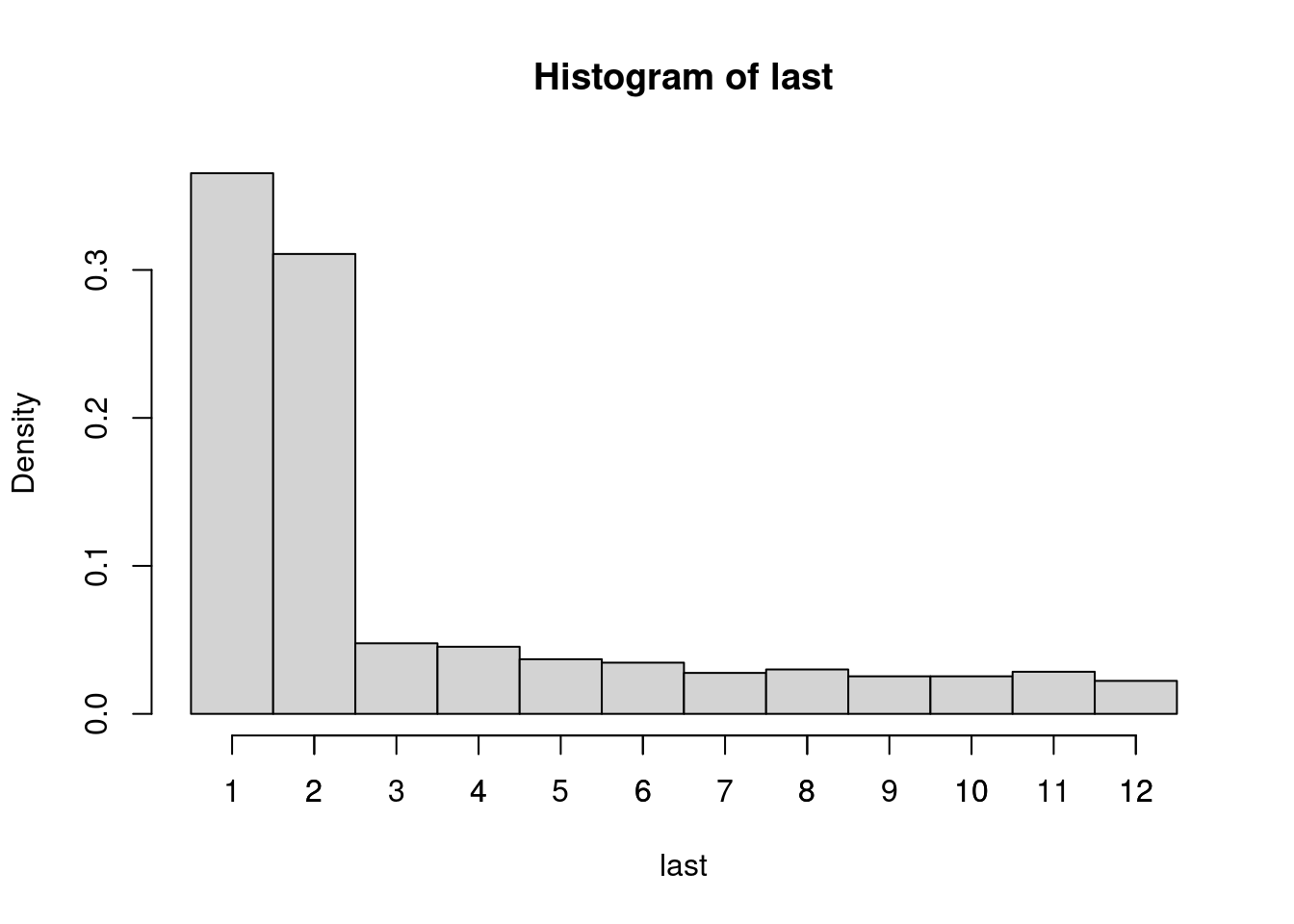
The absolute frequencies can be easily obtained with table(), showing that most customers have purchased something one or two months ago.

table(last)
## last
##   1   2   3   4   5   6   7   8   9  10  11  12 
## 475 404  62  59  48  45  36  39  33  33  37  29

The corresponding histogram can be plotted setting breaks in between the count values at \(0.5, 1.5, \dots, 12.5\). Subsequently, we also add a separate axis tick mark for each count \(1, 2, \dots, 12\).

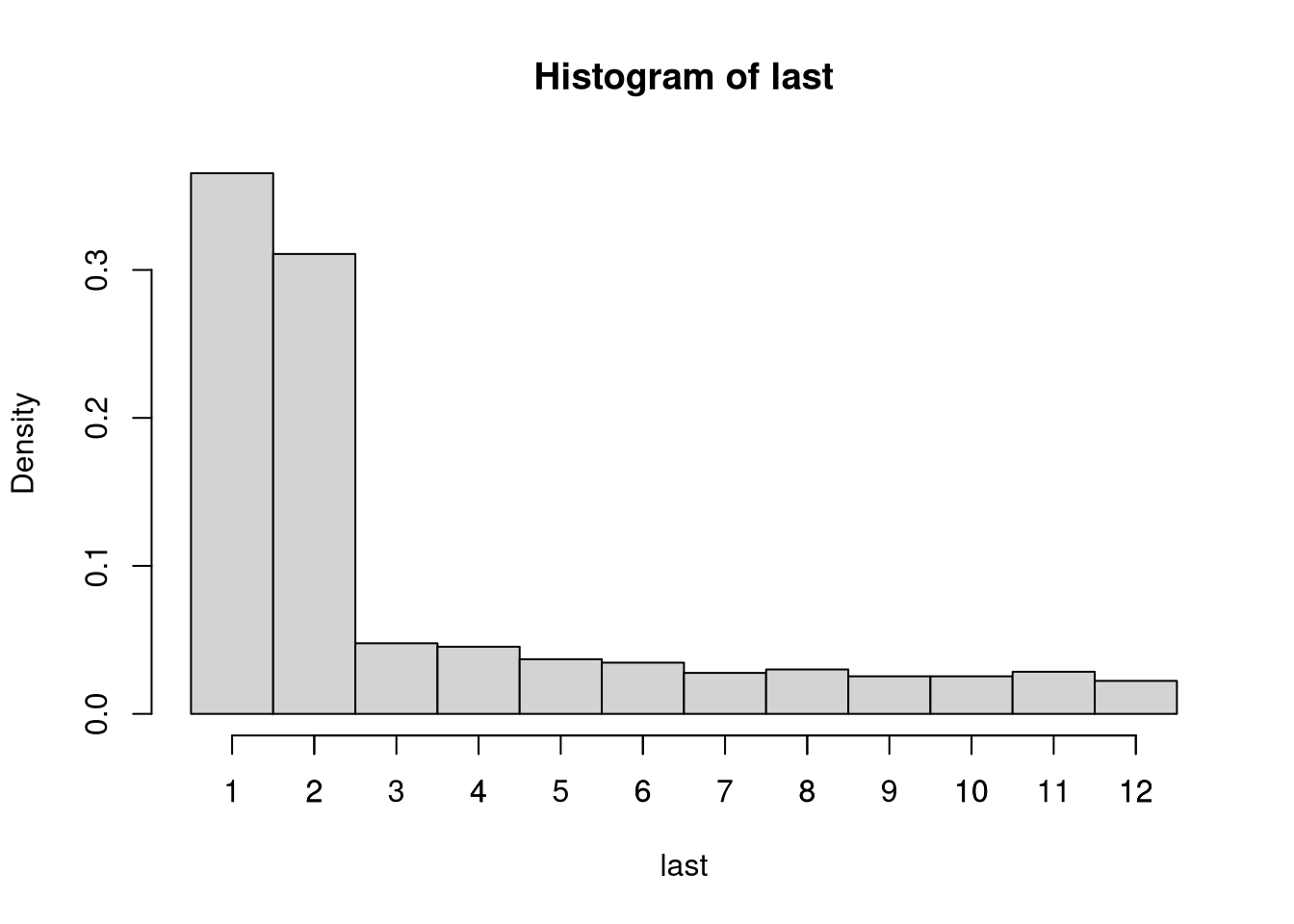
hist(last, breaks = seq(0.5, 12.5, by = 1), freq = FALSE)
axis(1, at = seq(1, 12, by = 1))

Python

The absolute frequencies can be easily obtained with value_counts(), showing that most customers have purchased something one or two months ago.

last = BBBClub['last']
print(last.value_counts())
## last
## 1     475
## 2     404
## 3      62
## 4      59
## 5      48
## 6      45
## 8      39
## 11     37
## 7      36
## 9      33
## 10     33
## 12     29
## Name: count, dtype: int64

The corresponding histogram can be plotted by

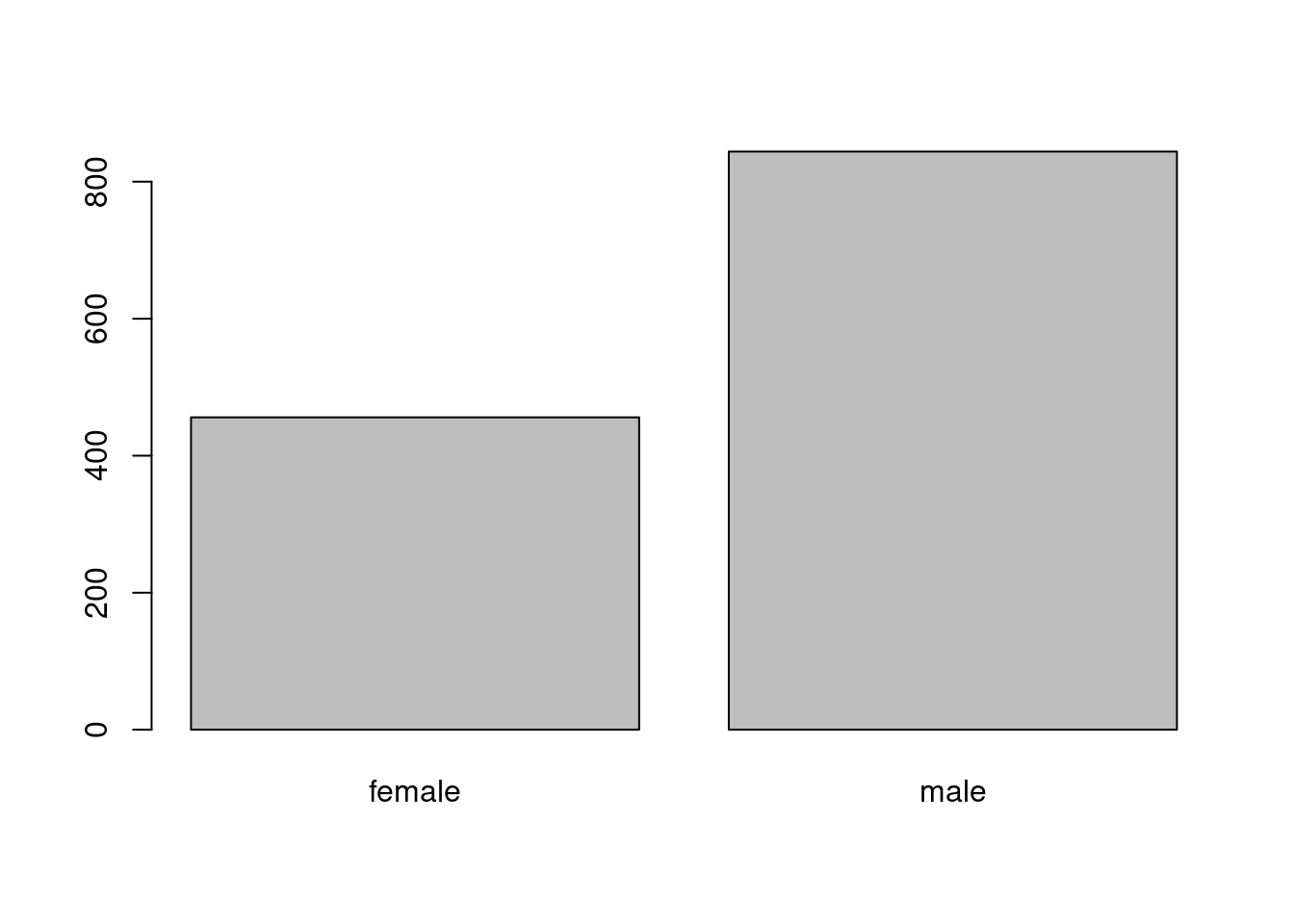
sns.histplot(data=last, stat="density")
plt.show()

4.3.3 One qualitative variable

For numerically summarizing a qualitative variable, we can compute the frequency table with:

R

If a qualitative variable is already coded appropriately as a factor in R, such as the gender variable in the BBBClub data, then many generic such as summary(gender) and plot(gender) automatically choose an appropriate methods. Below we show how these methods can be customized or supplemented with other tools.

We can simply compute the frequency table with either one of:

summary(gender)
## female   male 
##    456    844
table(gender)
## gender
## female   male 
##    456    844
Python
gender = BBBClub['gender']
print(gender.describe())
## count     1300
## unique       2
## top       male
## freq       844
## Name: gender, dtype: object
print(gender.value_counts())
## gender
## male      844
## female    456
## Name: count, dtype: int64

The corresponding relative frequencies can be computed for a proportions table.

R

By using prop.table() or simply by dividing with the number of observations:

tab <- table(gender)
prop.table(tab)
## gender
##   female     male 
## 0.350769 0.649231
tab/sum(tab)
## gender
##   female     male 
## 0.350769 0.649231
Python
tab = gender.value_counts()

print(tab/tab.sum())
## gender
## male      0.6492
## female    0.3508
## Name: count, dtype: float64

The corresponding bar plot can be plotted by:

R

Either applying plot() to the original factor variable or by barplot() to the frequency table.

plot(gender)
barplot(tab)

Hence, barplot(prop.table(tab)) could be used for a bar plot of the relative frequencies.

Python
sns.histplot(data=gender, stat="frequency")
plt.show()

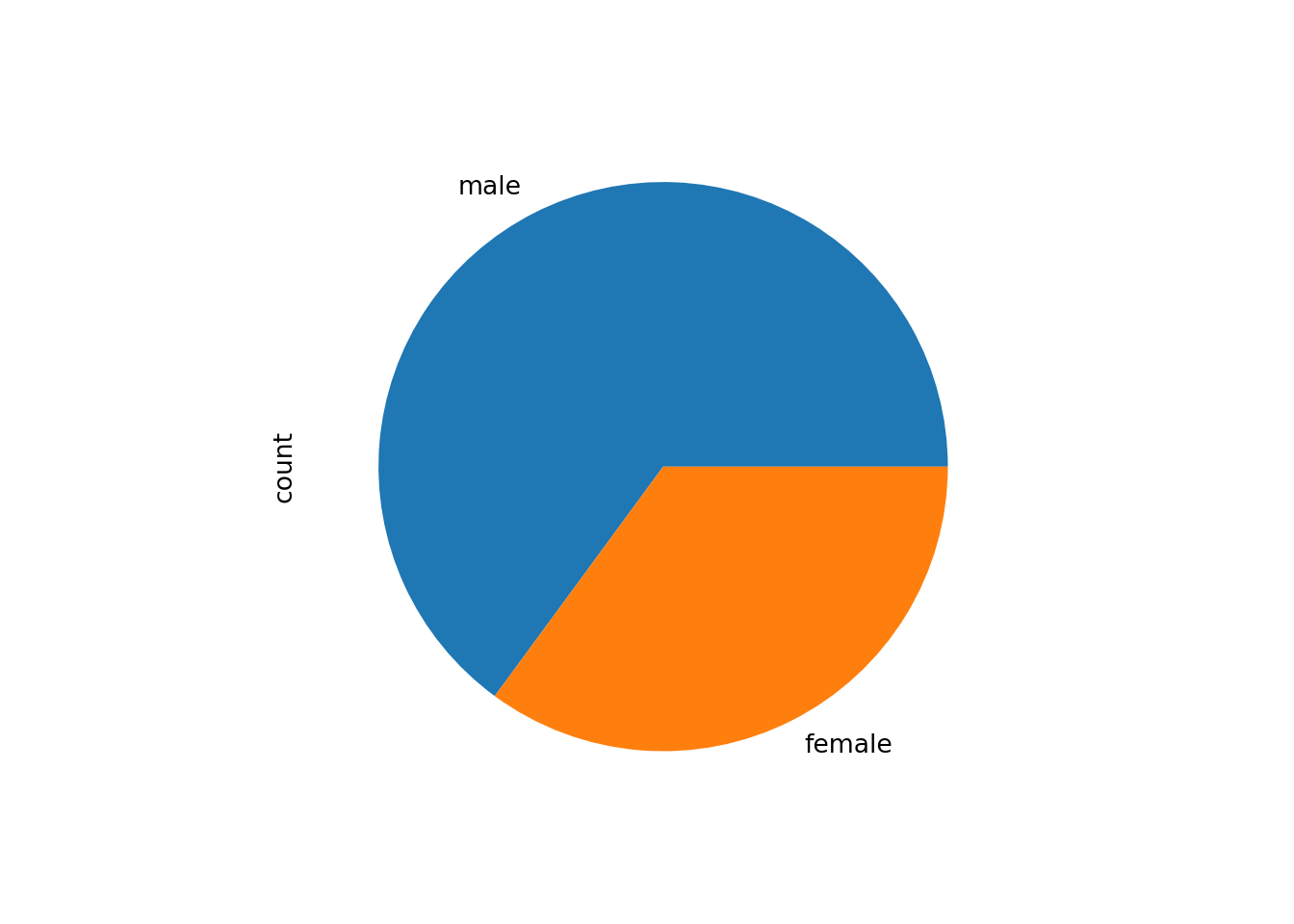
All of these show that about two thirds of the customers are male and one third female.

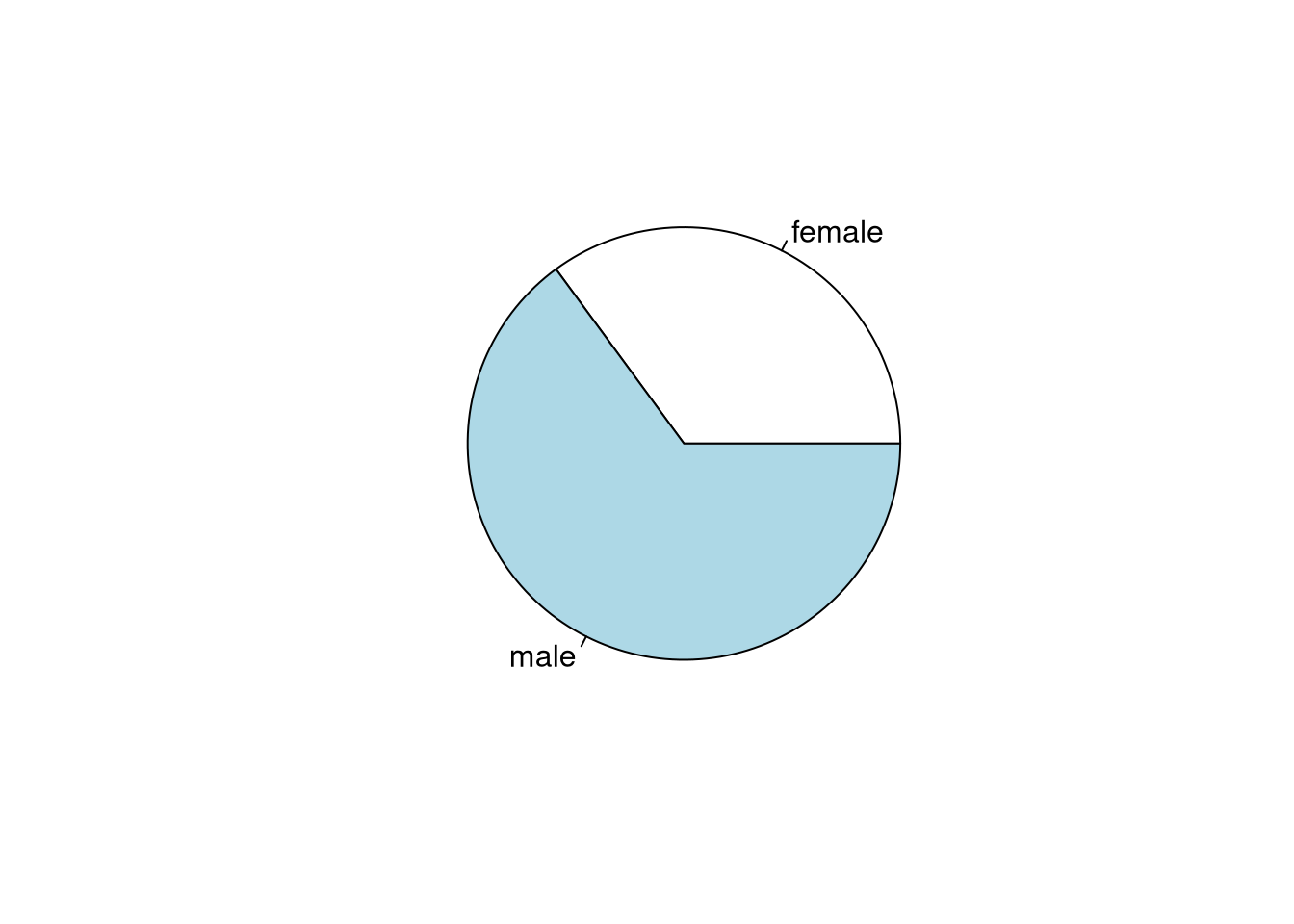
An alternative visual display is the pie chart. However, this is more suitable for conveying whether combinations of segments form a majority. For most other purposes a bar plot is preferable.

R

In base R, a pie chart can be drawn with pie().

pie(tab)

Python
tab.plot.pie()
# no seaborn version of pie plot
plt.show()

4.3.4 Two quantitative variables

The classical summary statistic for capturing the association between two quantitative variables is the Pearson correlation coefficient.

R

In R this is available in the cor() function as the default method = "pearson" along with alternative methods Spearman’s \(\varrho\) ("spearman") and Kendall’s \(\tau\) ("kendall"). The use argument enables various strategies for dealing with missing values in the data.

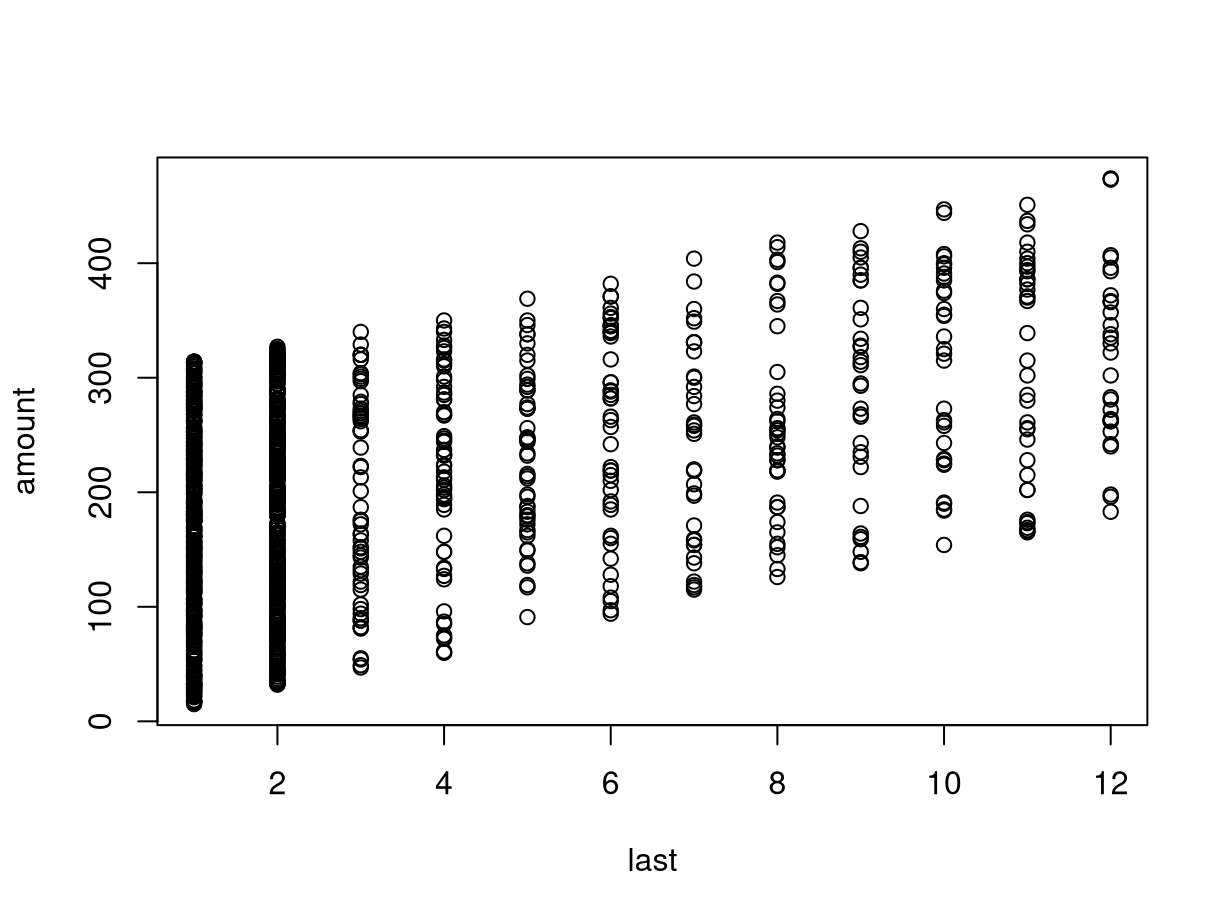
For the Bookbinders Book Club data we consider the association between the time since the last purchase and the total amount purchased so far.

cor(amount, last)
## [1] 0.452111
Python

In pandas this is available in the corr() function as the default method = 'pearson' along with alternative methods Spearman’s \(\varrho\) ('spearman') and Kendall’s \(\tau\) ('kendall').

print(amount.corr(other=last))
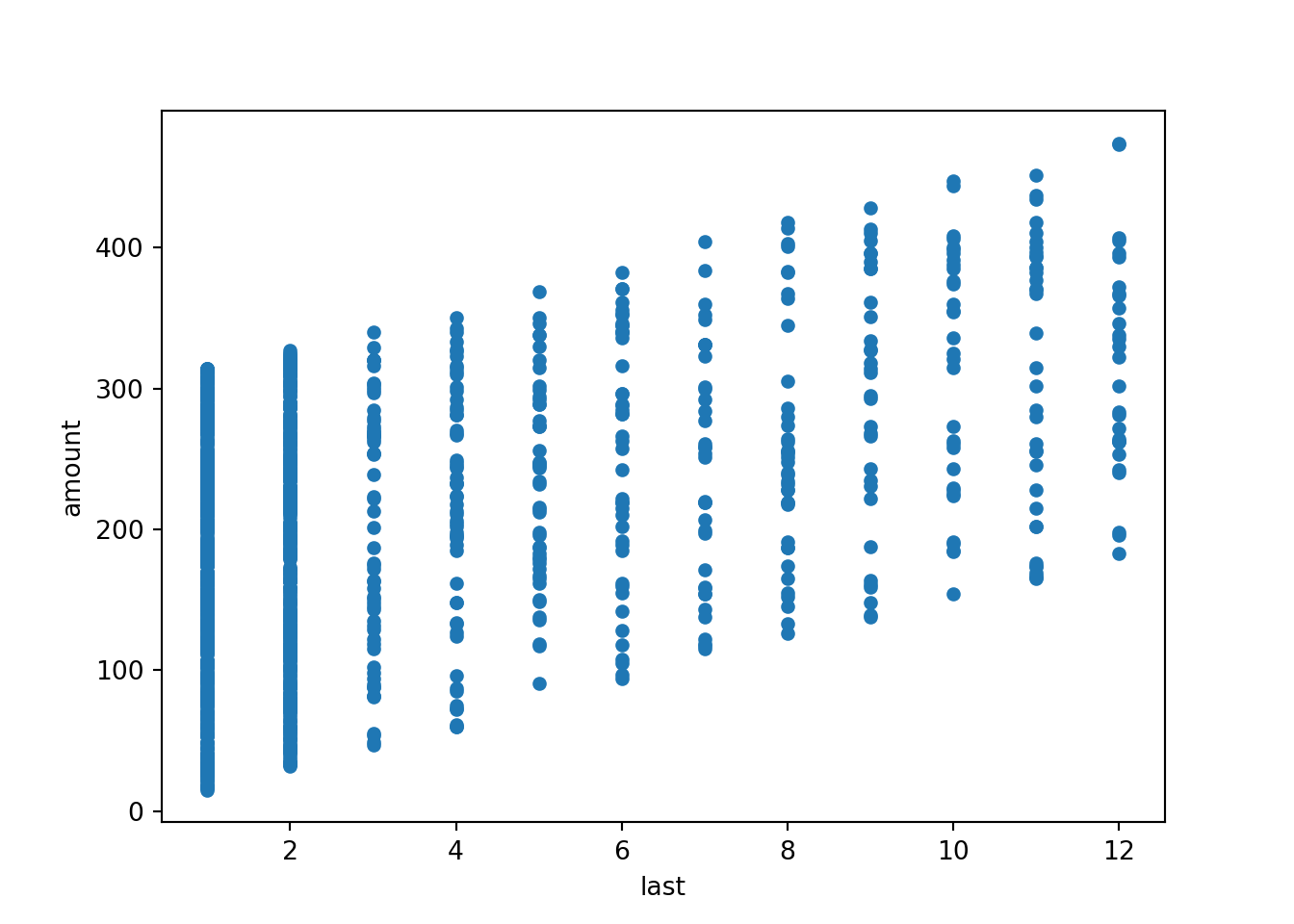
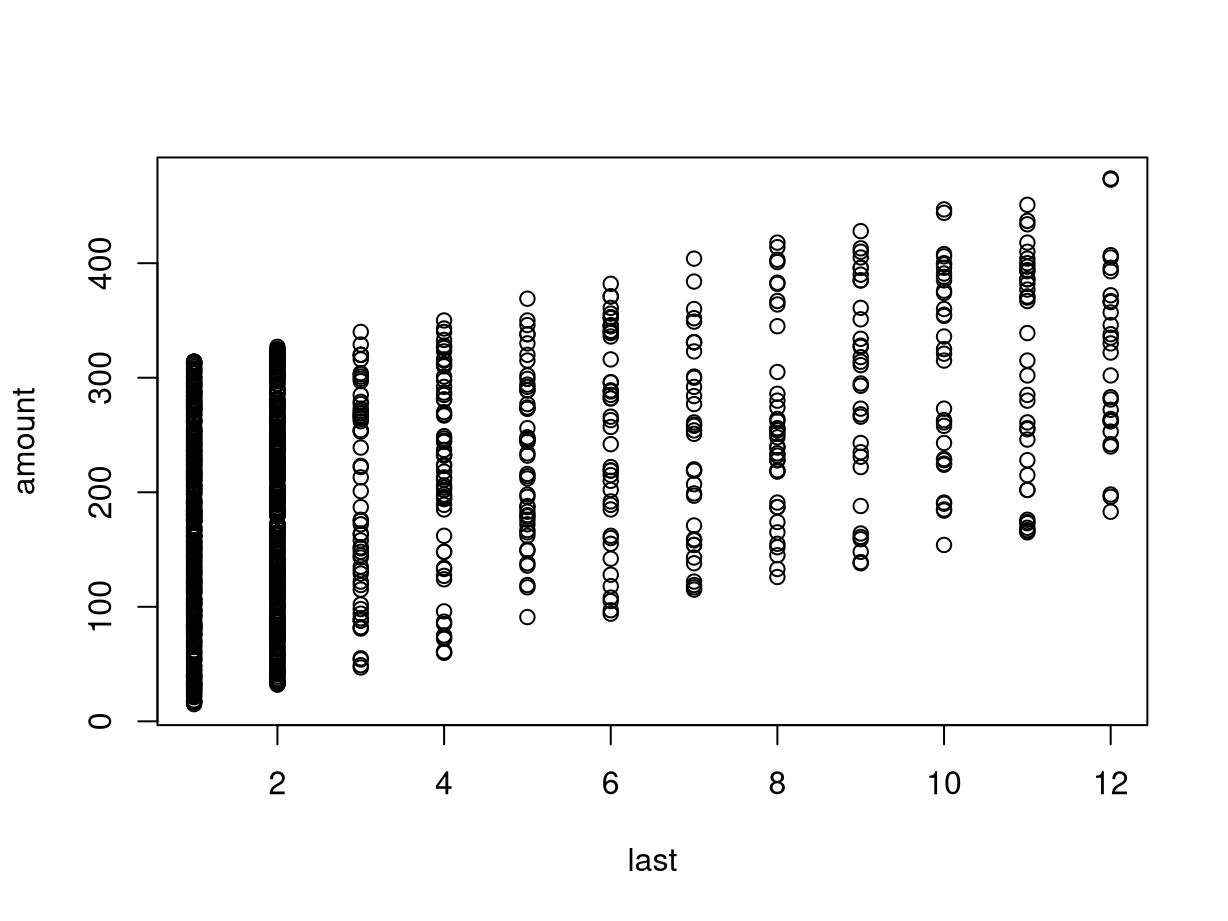
## 0.45211050943936815

These are positively correlated as customers who have been able to wait longer since their last purchase typically have purchased more (to fulfill the minimum purchase requirements of the book club).

This positive association can also be brought out graphically by the corresponding scatter plot below. This also shows clearly that last is actually discrete, leading to the vertical “stripes” in the plot.

R

The scatter plot can be generated in either of the two following ways:

plot(last, amount)
plot(amount ~ last, data = BBBClub)

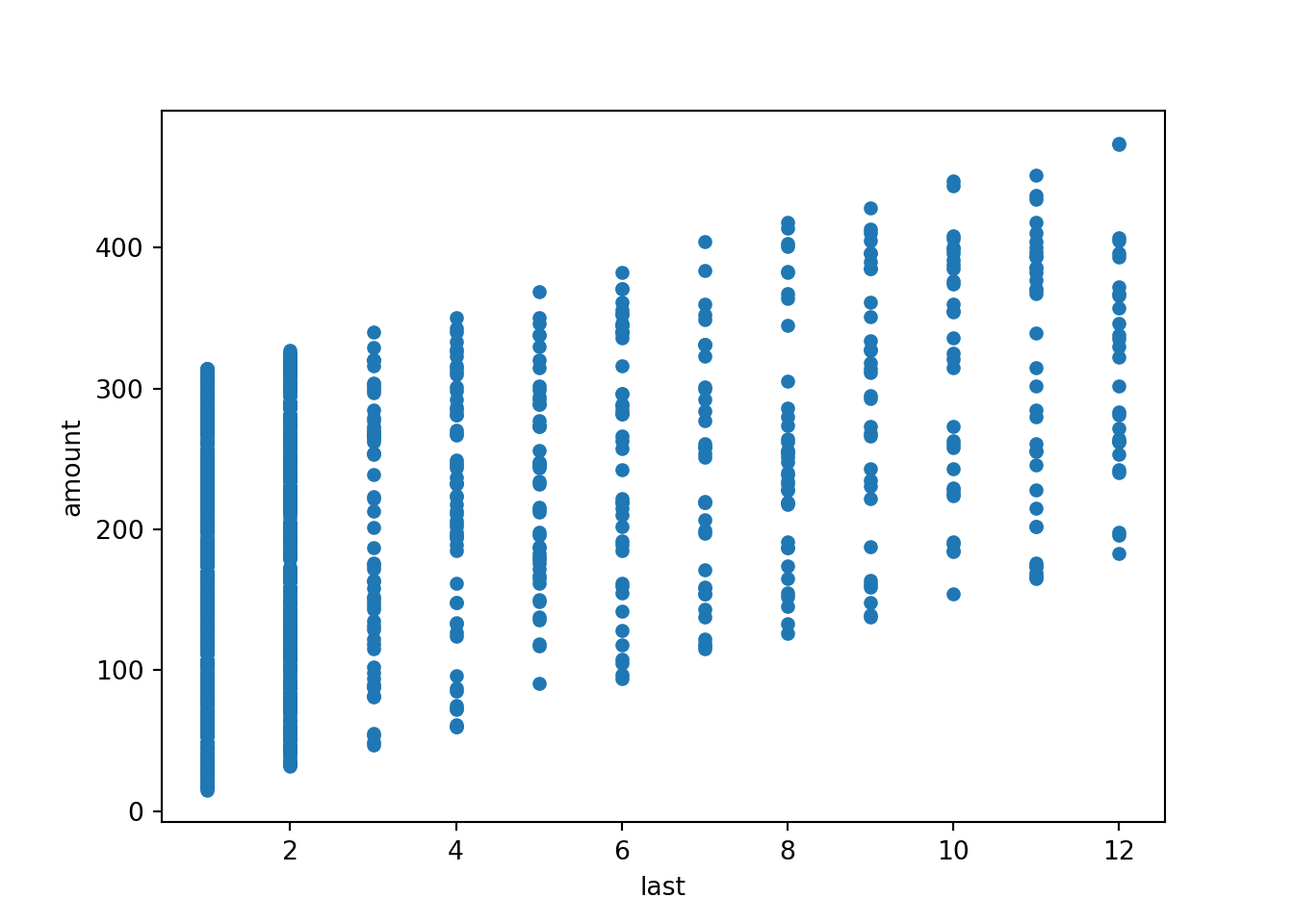
In the latter call a so-called formula is used to specify the plot setup. The ~ operator can be read as “explained by”, i.e., amount explained by last in this case. It has a number of advantages over the shorter plot(last, amount) call:

  • The relationship between the two variables is brought out more expressively by the formula which is also employed for specifying regression models.
  • The same formula specification can be used when one or both of the variables are qualitative rather than quantitative. The plot() method then chooses an appropriate visualization technique automatically (see below).
  • The data does not need to be attached but can be specified by the data argument, making the call more self-contained.
Python
BBBClub.plot.scatter(x='last', y='amount')
# seaborn version: sns.scatterplot(x=last, y=amount)
plt.show()

4.3.5 Dependent quantitative and explanatory qualitative variable

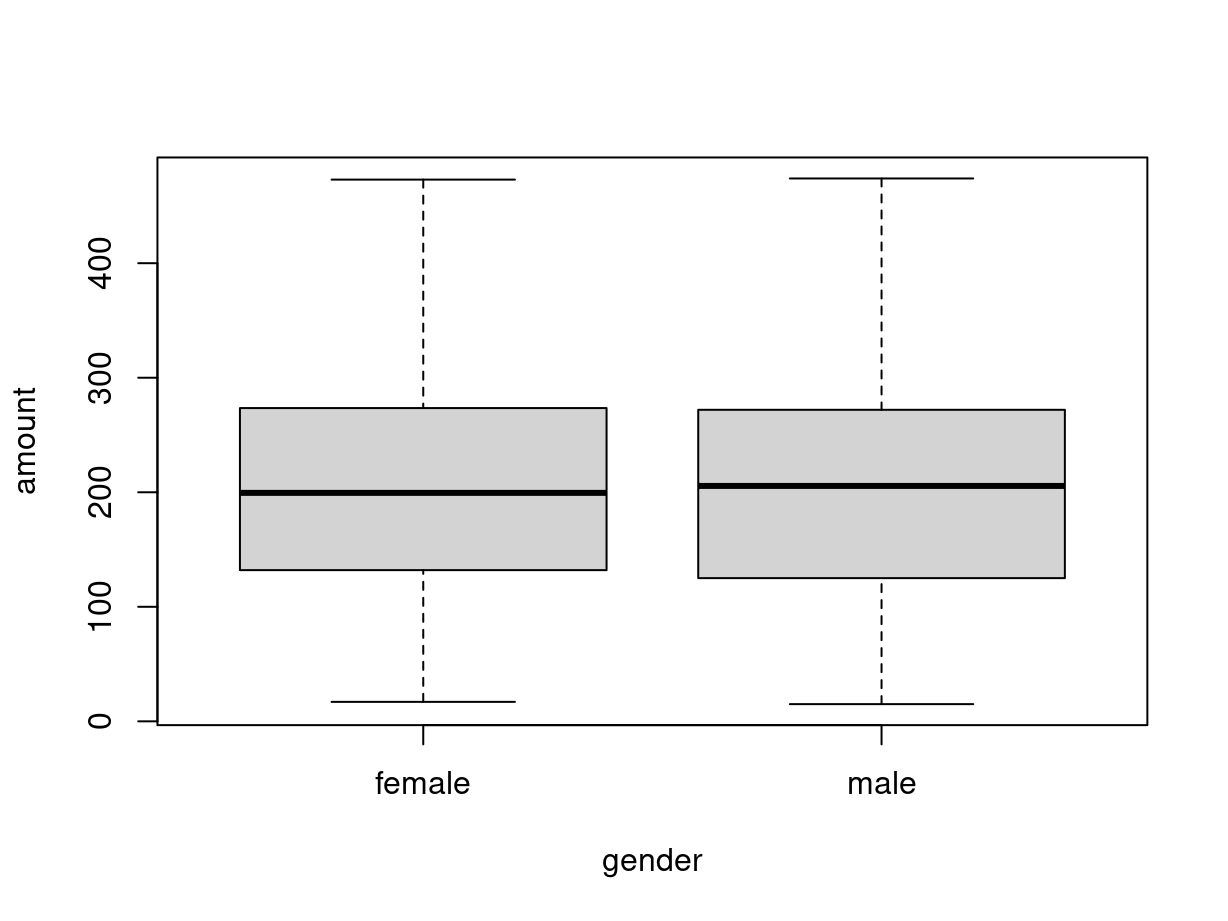
Visualization:

R

If the dependent variable is quantitative but the explanatory variable qualitative (i.e., a factor) in a formula-based visualization, the plot() method automatically chooses parallel box plots as an appropriate graphical display. Internally, this calls the boxplot() function.

plot(amount ~ gender, data = BBBClub)

Python
BBBClub.boxplot(column='amount', by='gender')
# seaborn version: sns.boxplot(x=gender, y=amount)
plt.show()

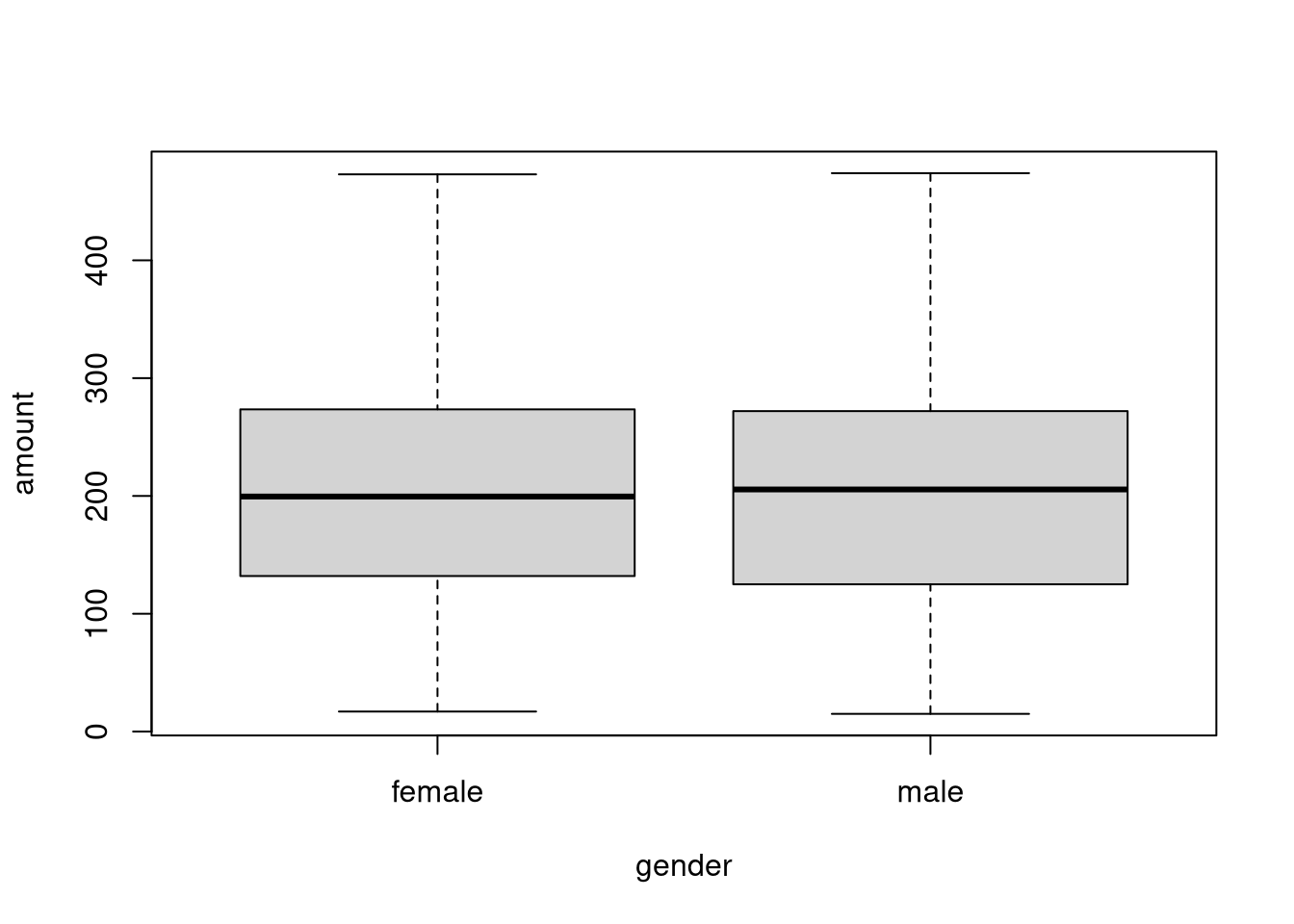
Here, it can be seen that the distribution of amount is essentially the same across both gender groups. Neither group spends more or less on average.

The corresponding groupwise statistics can be computed with…

R

In R, the tapply() function is used. The call tapply(y, x, FUN) takes a dependent y variable, an explanatory x variable, applies a FUNction in each of the x groups, and reports the result as a table (hence the name tapply()). The function to be applied in each of the subgroups can return a scalar or a vector value:

tapply(amount, gender, mean)
##  female    male 
## 203.491 200.223
tapply(amount, gender, summary)
## $female
##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##      17     132     200     203     273     473 
## 
## $male
##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##      15     125     206     200     272     474

Instead of just providing a single x variable, it would also be possible to provide a list() of explanatory variables. The function is then applied to each possible combination of the explanatory variables.

Python
print(BBBClub[['amount','gender']].groupby('gender').mean())
##           amount
## gender          
## female  203.4912
## male    200.2227
print(BBBClub[['amount','gender']].groupby('gender').describe())
##        amount                                                      
##         count      mean      std   min    25%    50%     75%    max
## gender                                                             
## female  456.0  203.4912  95.0974  17.0  132.0  199.5  273.25  473.0
## male    844.0  200.2227  94.4106  15.0  125.0  205.5  272.00  474.0

The results reflect what the boxplots have already shown above: The distribution of amount is essentially the same across both gender groups.

4.3.6 Two qualitative variables

The basic numeric description of the association between two qualitative variables is always the corresponding frequency or contingency table. For illustration, we explore whether men or women (variable gender) are more likely to purchase the advertised art book (variable choice):

R

In R the table() function can be used to generate such contingency tables - or alternatively the xtabs() function which has the advantage of a formula-based interface. However, note that there is no dependent variable in the xtabs() formula because all variables enter equally into the table.

table(gender, choice)
xtabs(~ gender + choice, data = BBBClub)
##         choice
## gender    no yes
##   female 273 183
##   male   627 217
Python
print(BBBClub[['gender', 'choice']].value_counts())
## gender  choice
## male    no        627
## female  no        273
## male    yes       217
## female  yes       183
## Name: count, dtype: int64

The raw absolute frequencies are hard to interpret because the two gender groups are not of equal size (about two thirds are men and one third women, see above). Several functions are available to visualize frequency tables.

R

R provides a number of functions that can transform and visualize frequency tables:

  • prop.table(): Compute relative frequencies of the overall table (default) or conditional on selected margins.
  • margin.table(): Sum frequencies across slected margins, e.g., for row or column sums.
  • ftable(): Print flat two-way tables based on underlying multi-way tables.
  • mosaicplot(): Visualization of multi-way contingency tables based on recursively splitting rectangles along margins based on conditional relative frequencies for given previous margins. Allows flexible specification of split order, direction, spacing, shading, etc.
  • spineplot(): Special case of the general mosaic display for two-way tables with a particular shading and spacing.

In the Bookbinders Book Club illustration, it is of interest how the conditional frequency of choice (second margin) given gender (first margin) differs:

tab <- table(gender, choice)
prop.table(tab, 1)
##         choice
## gender         no      yes
##   female 0.598684 0.401316
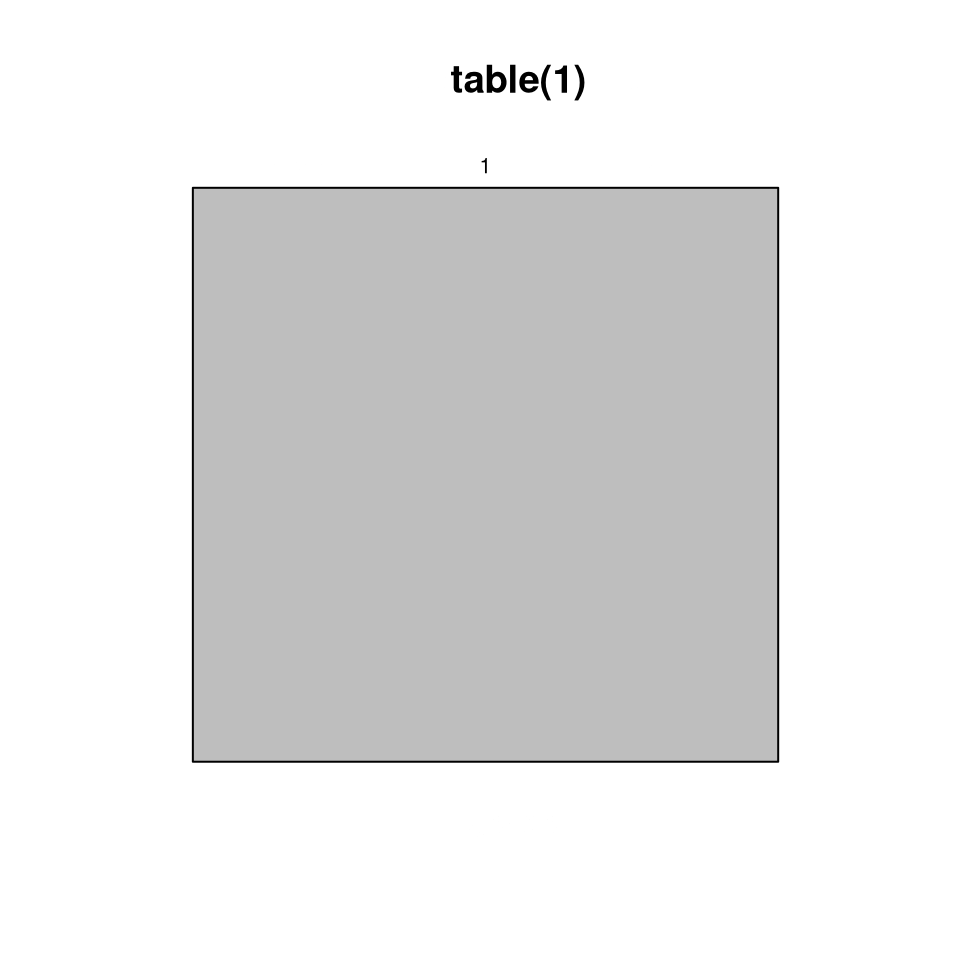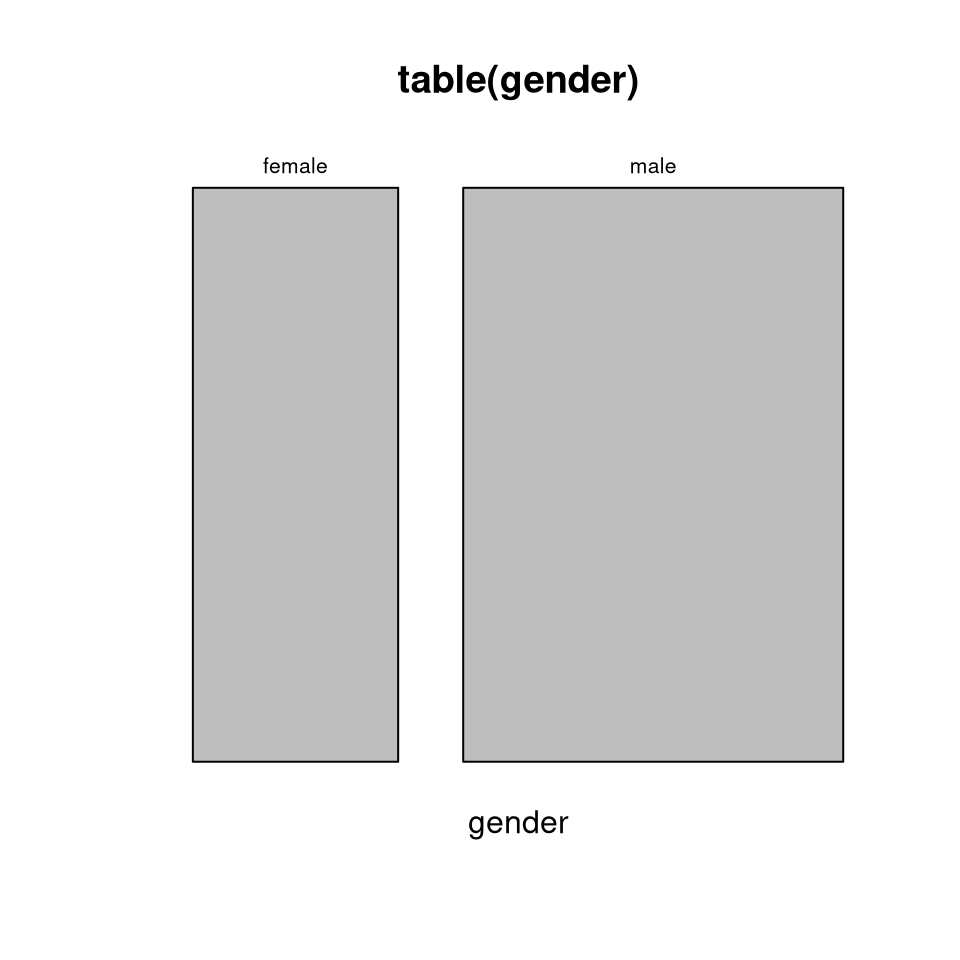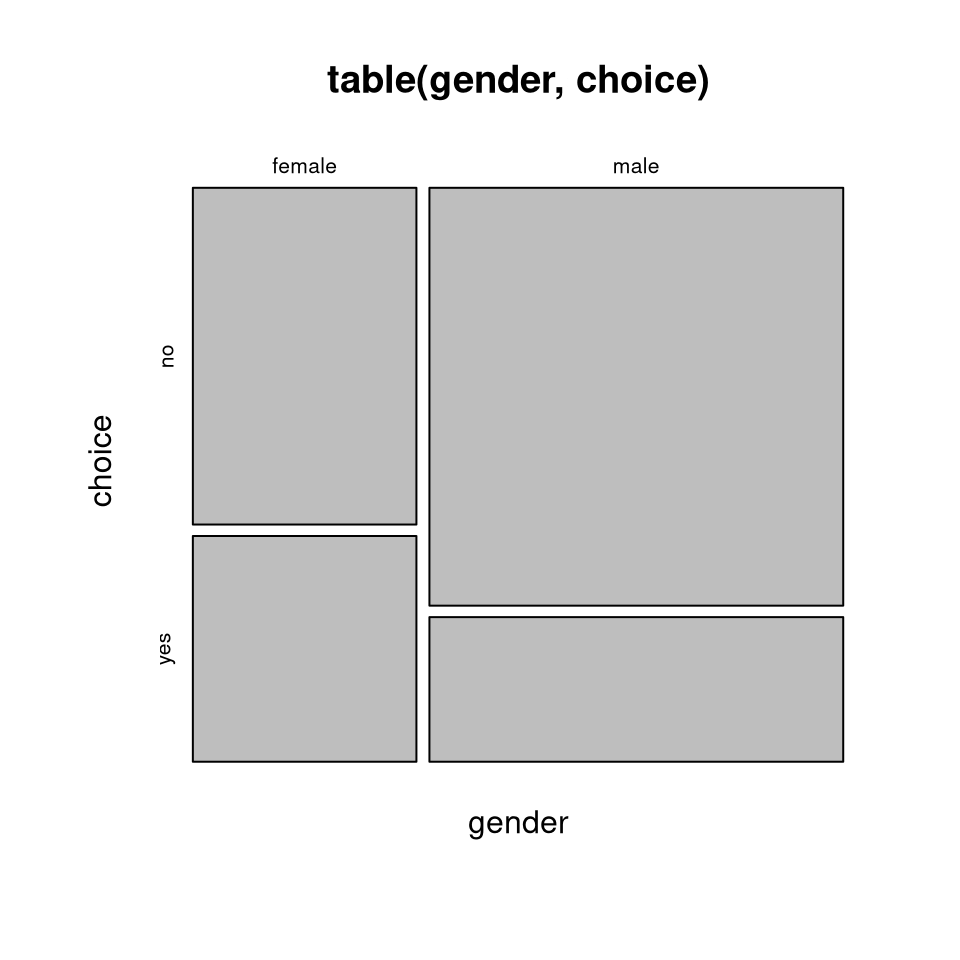
##   male   0.742891 0.257109

Clearly, the proportion of women purchasing the product (40.1%) is much higher than for the men (25.7%). The same can also be brought out by the corresponding mosaic plot or spine plot:

mosaicplot(tab)
spineplot(tab)

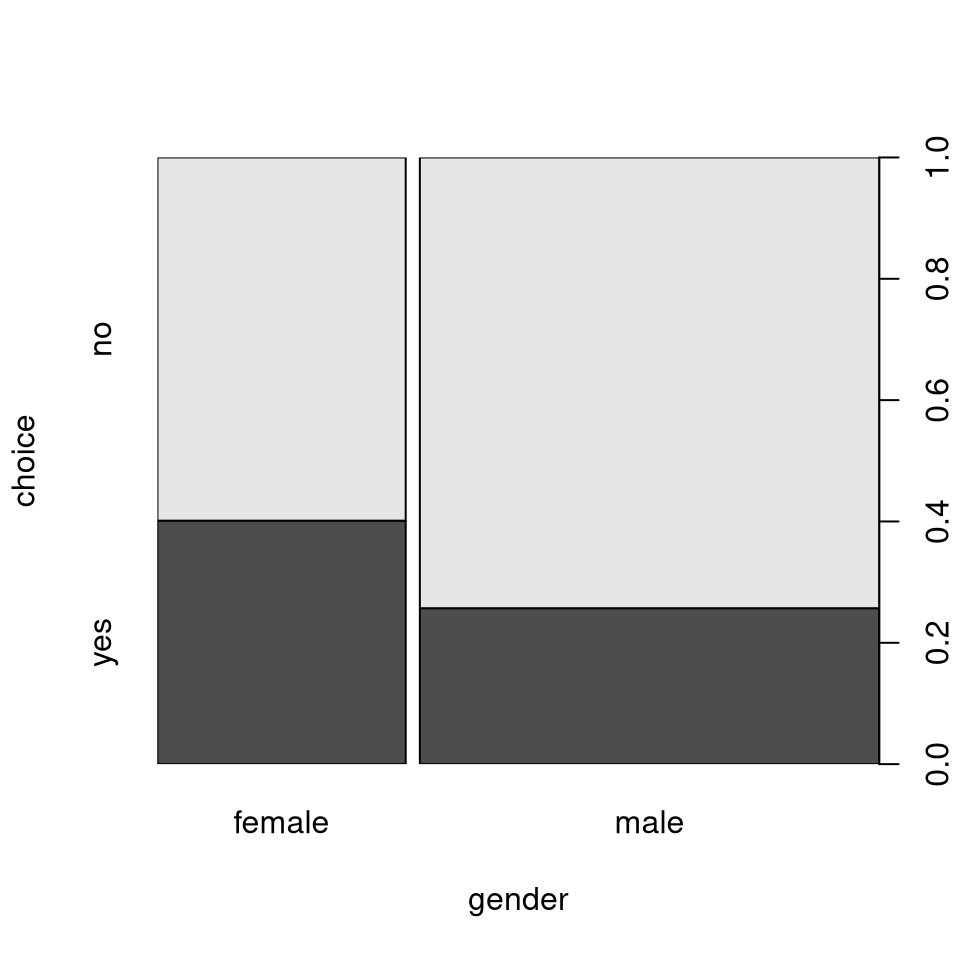
Note: To understand the construction of a mosaic/spine plot we can also take a rectangle representing 100%, split it first vertically by the marginal relative frequencies for gender, and then horizontally based on the conditional relative frequencies of choice given gender:

mosaicplot(table(1))
mosaicplot(table(gender))
mosaicplot(table(gender, choice))

The corresponding relative frequencies can be computed by hand via:

prop.table(margin.table(tab, 2))
## choice
##       no      yes 
## 0.692308 0.307692
prop.table(tab, 1)
##         choice
## gender         no      yes
##   female 0.598684 0.401316
##   male   0.742891 0.257109

Furthermore, the spineplot() also provides a formula interface and is called in the background by the general formula-based plot() method. Thus, the spine plot for the Bookbinders Book Club can also be generated “as usual” (and as in the sections above).

plot(choice ~ gender, data = BBBClub)

As a final remark, the spineplot() function (but not the plot() interface) return the visualized frequency table invisibly. Thus, without calling table() or xtabs() we can set up the plot and table above via:

tab <- spineplot(choice ~ gender, data = BBBClub)
Python
from statsmodels.graphics.mosaicplot import mosaic

# Reorder categories for mosaic plots
BBBClub['choice'] = BBBClub['choice'].astype('category');
BBBClub['choice'].cat.reorder_categories(['yes', 'no']);

grey_scale = lambda key: {'color': 'dimgrey' if 'yes' in key else 'lightgrey'} # Define a color map using lambda functionlambda key:

mosaic(data=BBBClub, index=['gender', 'choice'], properties=grey_scale, gap=0.02, statistic=True);
plt.show()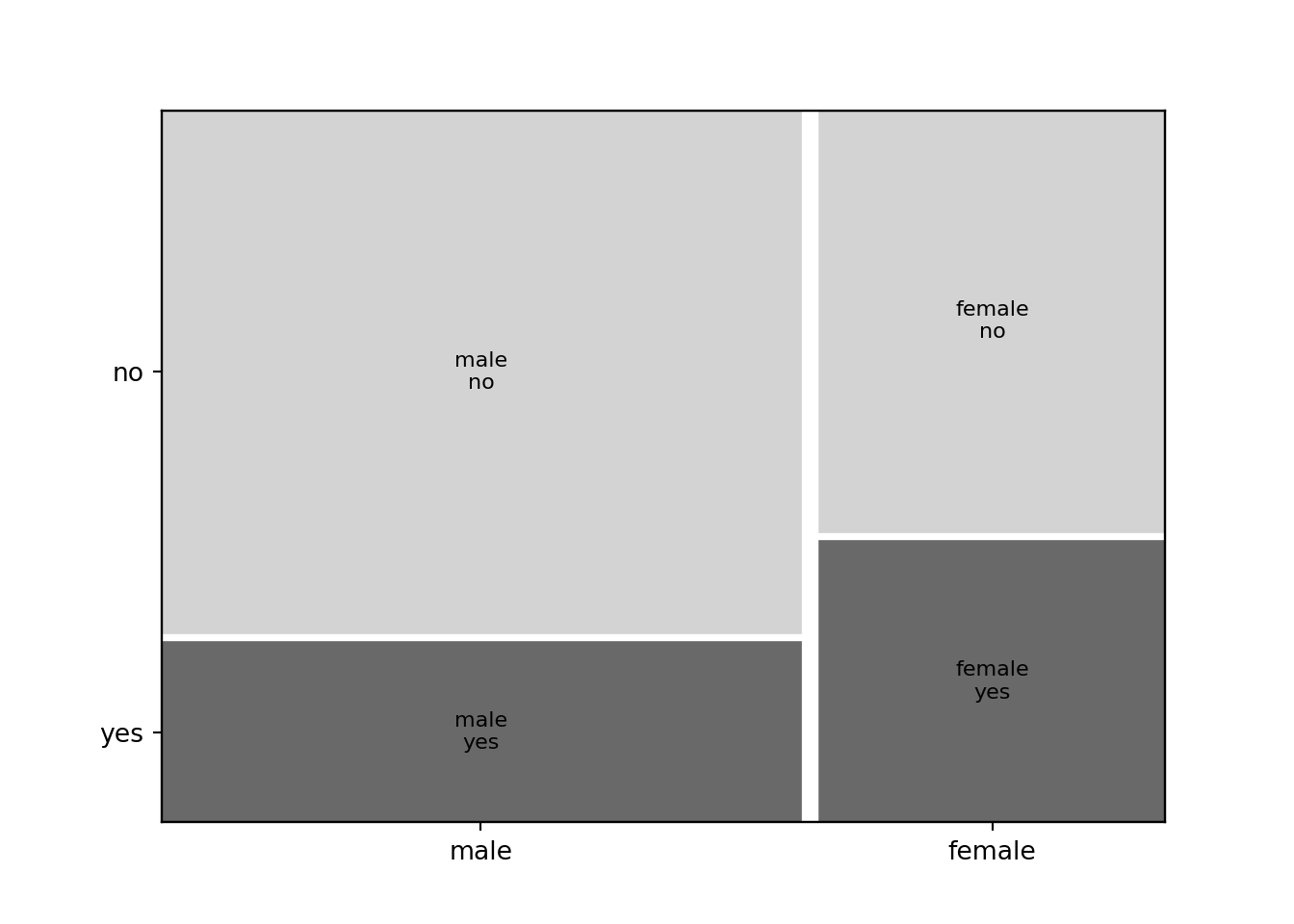

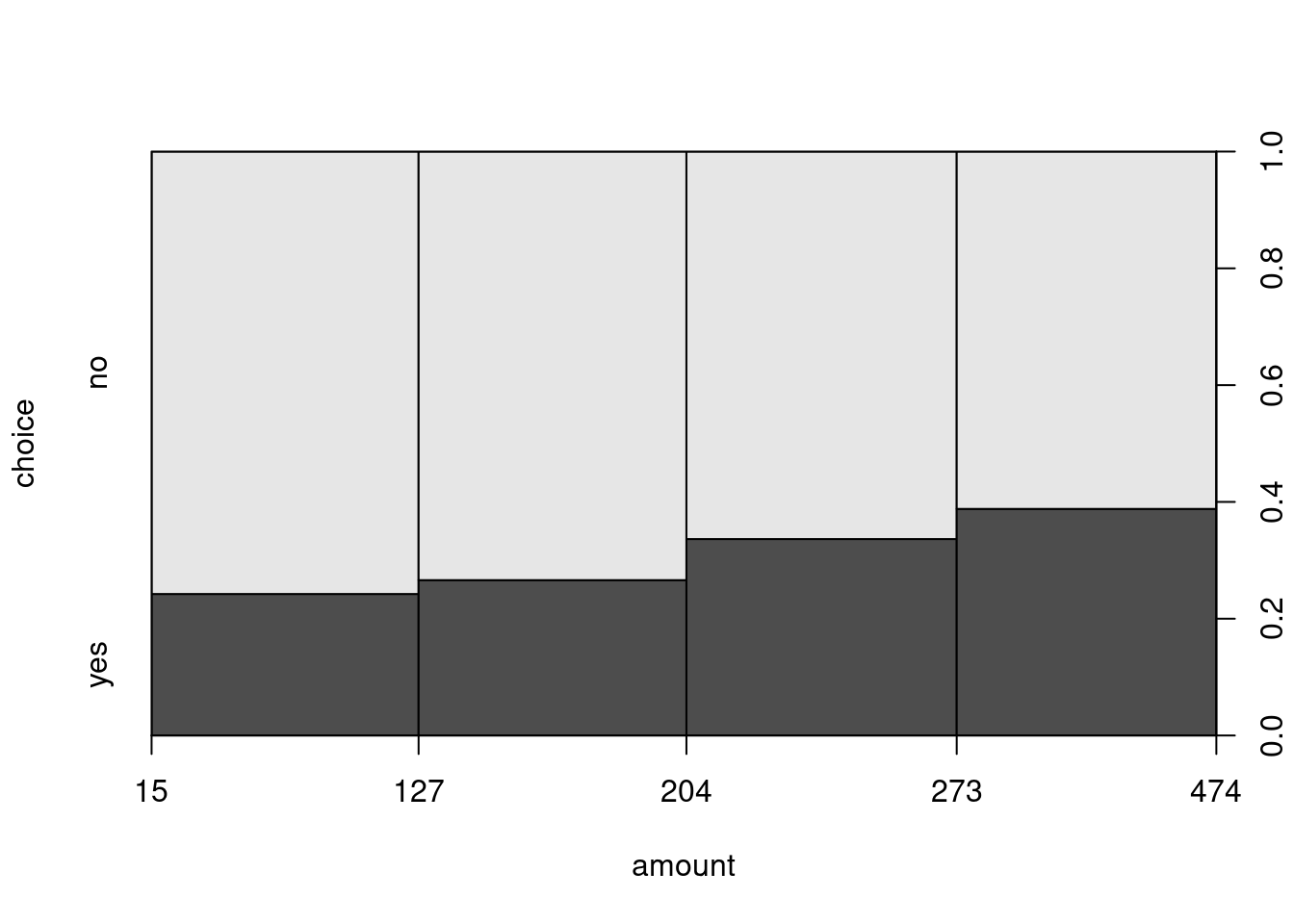
4.3.7 Dependent qualitative and explanatory quantitative variable

The situation with a dependent qualitative and explanatory quantitative variable is essentially handled like the setup with two qualitative variables by breaking the quantitative variable up into separate bins or intervals. This is essentially the same idea that the histogram uses for visualization.

R

For visualization, this handled automatically by the spineplot() function which is again interfaced through the general formula-based plot() method. As an illustration we show how the conditional purchase frequency for the advertised art book (variable choice) increases along with total amount spent so far:

plot(choice ~ amount, data = BBBClub)

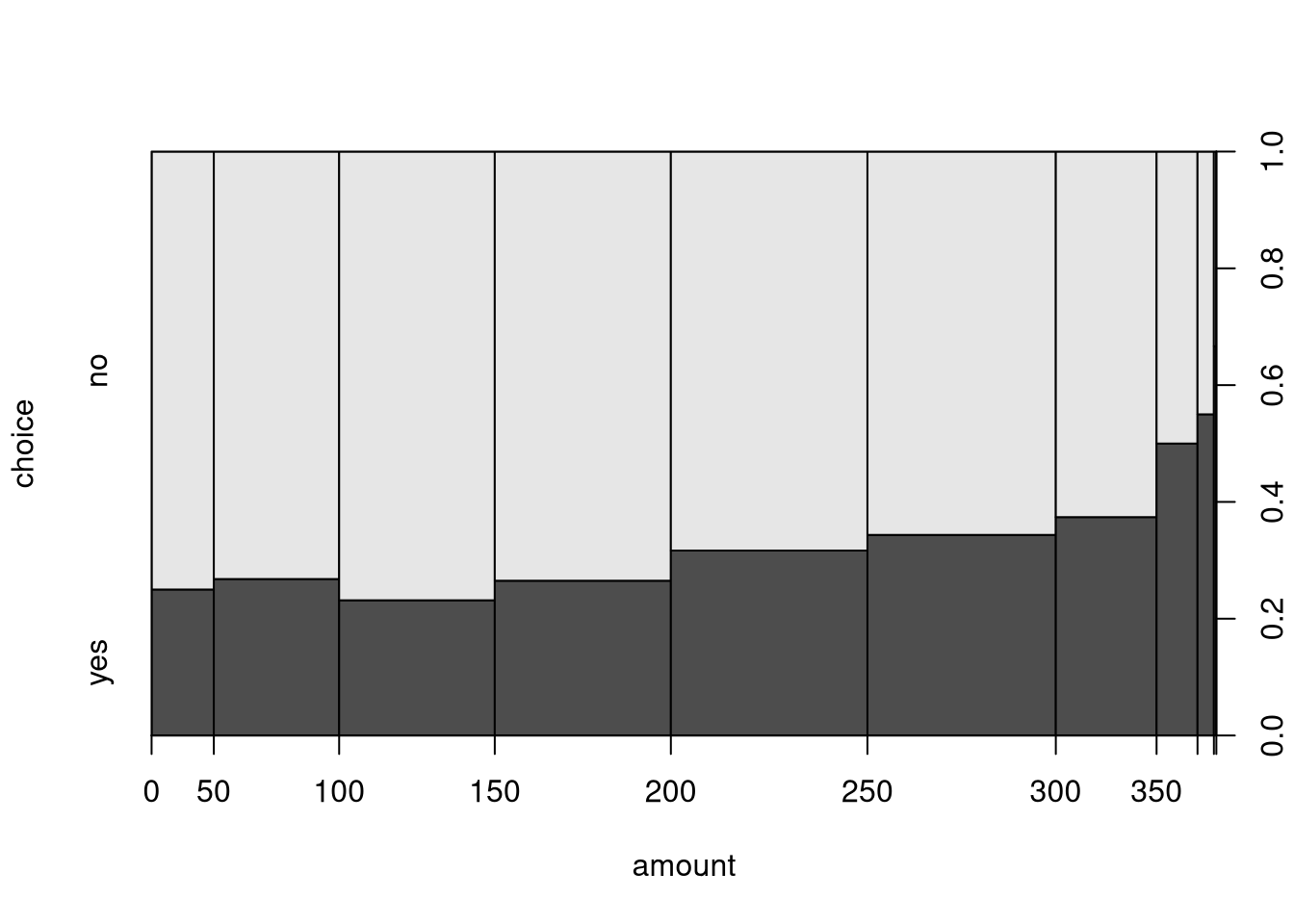
By default, the interval bins are chosen equidistantly as in hist(), yielding a somewhat distorted x-axis. While the distance on the x-axis always corresponds to fifty dollars, the marginal distribution differs substantially with amounts between 100 and 300 being much more frequent (i.e., yielding wider bins).

Alternatively, the breaks for the intervals can also be modified. For illustration, we employ the five-point summary yielding bins that approximately contain 25% of observations each (but are not equidistant on the dollar scale).

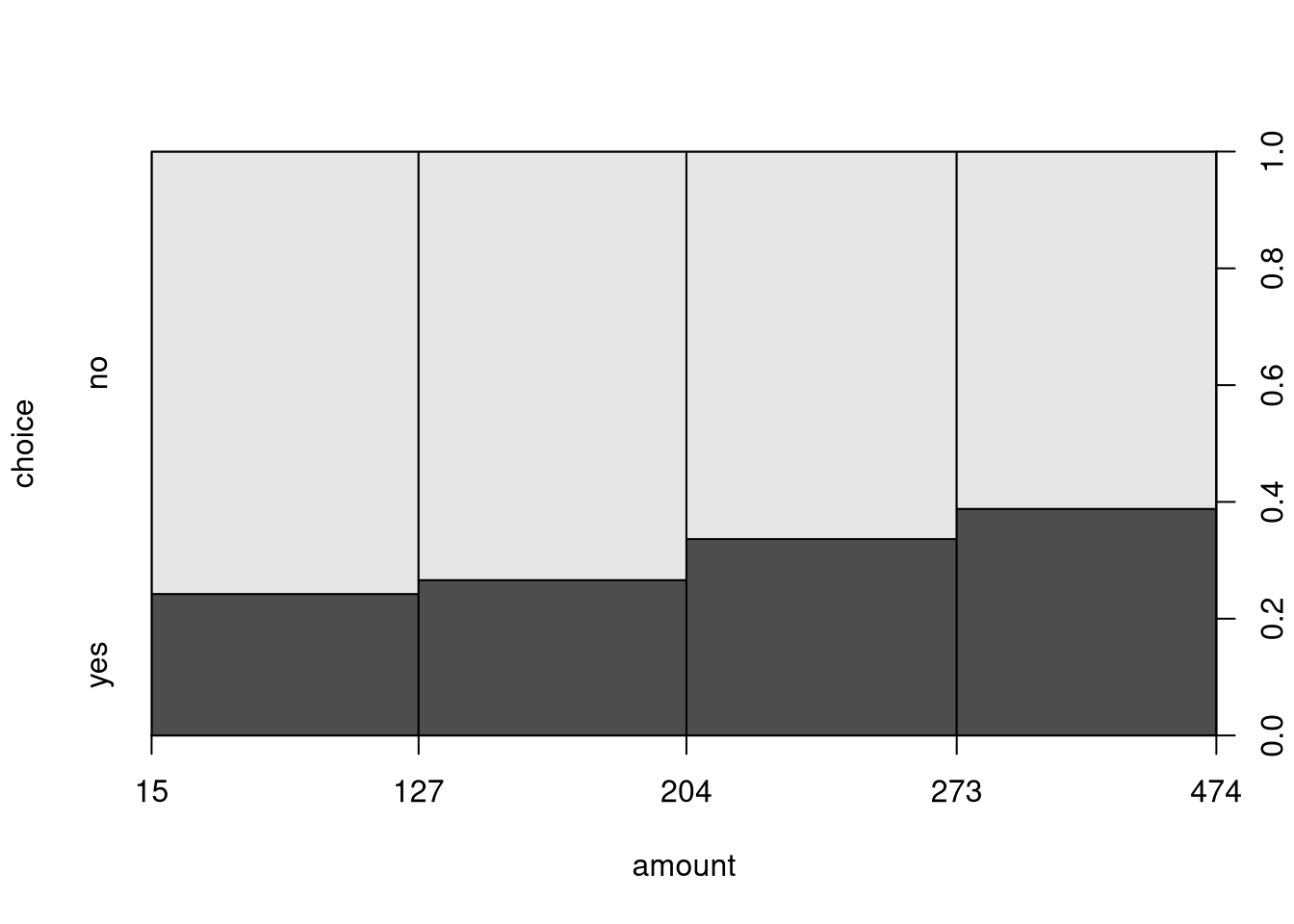
plot(choice ~ amount, data = BBBClub, breaks = fivenum(amount))

When calling spineplot() directly (rather than the plot() interface), the underlying contingency table is again returned invisibly. It can also be constructed “by hand” by first cut()-ting the amount variable to a factor and then using table() and prop.table() as in the previous section.

amount2 <- cut(amount, fivenum(amount), include.lowest = TRUE)
summary(amount2)
##  [15,127] (127,204] (204,273] (273,474] 
##       326       327       330       317
tab <- table(amount2, choice)
tab
##            choice
## amount2      no yes
##   [15,127]  247  79
##   (127,204] 240  87
##   (204,273] 219 111
##   (273,474] 194 123
prop.table(tab, 1)
##            choice
## amount2           no      yes
##   [15,127]  0.757669 0.242331
##   (127,204] 0.733945 0.266055
##   (204,273] 0.663636 0.336364
##   (273,474] 0.611987 0.388013

Concluding remark

As argued initially: When attaching a data frame, one should be very careful to also detach it again before proceeding with other analyses. Otherwise, multiple attached data frames are a common source of confusion.

detach(BBBClub)
Python
BBBClub['amount_bin'] = pd.cut(BBBClub['amount'], fivenum(BBBClub['amount'])) # Bin 'amount' samples
mosaic(data=BBBClub, index=['amount_bin', 'choice'], properties=grey_scale, gap=0.02, statistic=True);
plt.show()

print(BBBClub['amount_bin'].describe())
## count               1299
## unique                 4
## top       (204.0, 273.0]
## freq                 330
## Name: amount_bin, dtype: object
print(BBBClub[['amount_bin', 'choice']].value_counts())
## amount_bin      choice
## (15.0, 127.0]   no        246
## (127.0, 204.0]  no        240
## (204.0, 273.0]  no        219
## (273.0, 474.0]  no        194
##                 yes       123
## (204.0, 273.0]  yes       111
## (127.0, 204.0]  yes        87
## (15.0, 127.0]   yes        79
## Name: count, dtype: int64