Chapter 4 Vectors

In this chapter we will learn about one of the most basic objects in R, so-called vectors. Before starting, let us do a quick detour to “objects”.

4.1 Objects in R

R is an object-oriented programming language with the fundamental design principle: Everything in R is an object. In R, objects can be:

Variables (e.g., a, b, result).
Functions (e.g., mean(), max(), sin()).
Connection handlers.
…

Remember the very simple example from the chapter First Steps where we calculated \(a^2\) as follows?

a <- 5
a^2

We assign 5 to a. This automatically creates a new object (a) and stores the desired value in it (here 5).

Object orientation: All objects in R have a specific class that can have a set of class-specific attributes as well as methods for certain generic functions. In this simple example, a gets a numeric vector of length 1 (i.e., containing one numeric value).

Know the basics!

Vectors are sometimes also referred to as the ‘nuts & bolts’ in R as they build the basis for all complex objects such as data frames or fitted regression models. The image below shows a (simplified) schematic overview of how various more complex objects (on the right hand side) are based on vectors (on the left hand side).

Figure 4.1: Simplified schematic overview of how different R objects, covered in this book, are connected.

Frequently-used data types can also be distinguished by their dimensionality (1-d, 2-d, n-d) and whether they are homogenous (with all elements of the same type) vs. heterogenous (with elements of potentially different types).

Dimension	Homogenous	Heterogenous
1	Atomic vectors	Lists
2	Matrix	Data frame
\(\ge 1\)	Array

In this course, we will learn about vectors (atomic vectors), matrices (2-d arrays), factors, date and date time objects, lists, and data frames. In other situations, you will most certainly come across many other more complex objects, but keep in mind that most of them are created by using basic vectors (i.e., lists and atomic vectors).

Thus: Knowing these basics is essential to becoming a good programmer!

Print objects

When working on the interactive R console we can always print objects to see what is stored in them. This can be done by simply entering the name of the object and pressing enter:

## [1] 5

What happens is ‘implicit printing’ (we have not explicitly asked for it). Explicit printing would be if we call the print() function:

print(a)

## [1] 5

Both have the same effect when working on the interactive console. When writing scripts, the print() function becomes more important as implicit printing will no longer work (or only in special situations).

One way to (i) create new objects and (ii) directly print them is by adding another pair of round brackets around the command. Instead of doing it in two steps

a <- 5^2
a

## [1] 25

we can call (a <- 5^2). The additional brackets cause implicit printing because the result of the assignment to a is evaluated, thus creating the same effect as the two separate lines above.

(a <- 5^2)

## [1] 25

This is sometimes useful for brevity, avoiding additional typing and saving some space in the displayed code.

4.2 (Atomic) vectors

A vector is nothing else than a sequence of elements of a certain type. R distinguishes vectors with two different modes.

Atomic vectors: All elements must have the same basic type (e.g., numeric, character, …).
Lists: Special vector mode. Different elements can have different types.

Lists are deferred to a later chapter and are not important for now. Also, we follow standard albeit somewhat sloppy jargon and refer to atomic vectors simply as vectors while referring to vectors of mode list explicitly as lists (rather than vectors).

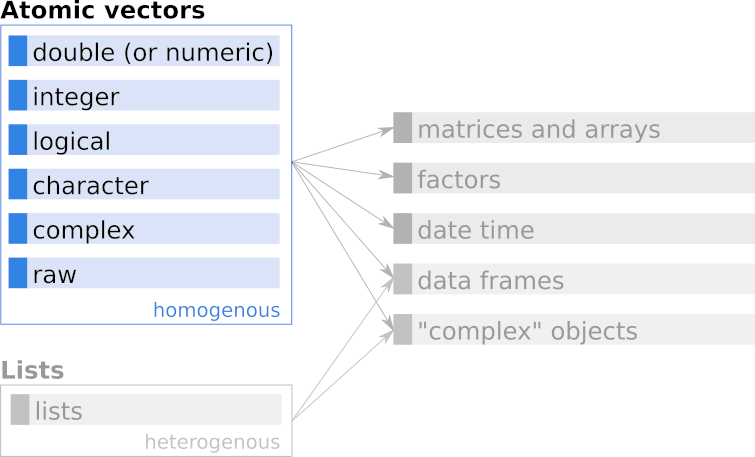
Figure 4.2: Simplified schematic overview of vectors in R which are covered in this chapter.

(Atomic) vectors are the most basic objects in R as they can contain only data of one type (e.g., only numeric values, or only character strings, etc.). Six different types of data can be stored in atomic vectors.

Table 4.1: Six types of atomic vectors in R. Only the first four (double, integer, logical, and character) are discussed and used in this book.
	Type	Example	Comment
1	double (or numeric)	`-0.5`, `120.9`, `5.0`	Floating point numbers with double precision
2	integer	`-1L`, `121L`, `5L`	“Long” integers
3	logical	`TRUE`, `FALSE`	Boolean
4	character	`"R"`, `"5"` or `'R'`, `'5'`	Text
5	complex	`-5+11i`, `3+2i`, `0+4i`	Real+imaginary numbers
6	raw	`01`, `ff`	Raw bytes (as hexadecimal)

Important vector functions

In programming, functions are used to perform a specific task, e.g., manipulate an object, calculate a derived quantity, or investigate existing objects. A few of the most important ones for creating and investigating simple vectors are:

c(): Combines multiple elements into one atomic vector.
length(): Returns the length (number of elements) of an object.
class(): Returns the class of an object.
typeof(): Returns the type of an object. There is a small (sometimes important) difference between typeof() and class() as we will see later.
attributes(): Returns further metadata of arbitrary type.

First example: Let us start with a simple example and assign (<-) the value 1.5 (a numeric floating point number) to an object named x.

x <- 1.5

We can now use the functions above to investigate this vector and check what the functions return.

length(x)      # Length of the vector.

## [1] 1

class(x)       # What is the class of the object?

## [1] "numeric"

typeof(x)      # What is the type of this vector?

## [1] "double"

Length: 1.5 is a single numeric value. Thus, x is a vector with only one element and has length 1. In R, a single element is always a vector of length 1, there is no special object for single values.
Class: The object is of class “numeric”.
Type: While the class is “numeric” the underlying type is “double”. We will come back to what that actually means later.

Second example: We create a new atomic vector with two elements, both integers (as indicated by the L suffix for long integers). c() is the function which combines both values to a new vector, which we (again) store in x. Whatever has been in x previously will be lost, as we overwrite the object.

x <- c(111L, 555L)     # Create the vector; overwrite 'x'
length(x)              # Checking length

## [1] 2

class(x)               # Checking class

## [1] "integer"

typeof(x)              # Checking the type

## [1] "integer"

Length: As expected, length() now returns 2 as we have stored two elements.
Class and type: Both functions return "integer".

Third example: As a last example let us create a character vector. A character (or character string) is nothing else but “text”, declared in R either by double quote "..." or single quotes '...'. In this case we store two character strings with short text snippets in a new vector called y:

y <- c("this is", "just some text")
length(y)

## [1] 2

class(y)

## [1] "character"

typeof(y)

## [1] "character"

Length: The length is 2 as our atomic vector y contains two character strings ("this is" and "just some text"). Note that length() does not count the number of individual characters, but the number of elements in our vector y. Feel free to try nchar(y) and note the difference.
Class and type: Twice the same, class and type are identical.

Double (or numeric)

One atomic data class is the double class (double precision floating point values). Double is actually not often used in R, objects of type double are simply called numeric and the class of floating point numbers will be "numeric".

x <- 1.5
x

## [1] 1.5

Note: the number 10 will also be numeric (double) as 10 is interpreted as 10.000.

(x <- 10)

## [1] 10

class(x)

## [1] "numeric"

Integers

A second atomic class is the integer class. Integers can explicitly be defined using the L (“Long”) suffix. While 10 will be double (or numeric; 10.0), 10L defines an integer (natural number).

(x <- 10L)

## [1] 10

class(x)

## [1] "integer"

This is not important most of the time when you are using R. Except when it is! There are some situations where integers are required!

Logical

Logicals are rather simple as they can only take up two different values: either TRUE or FALSE.

(x <- TRUE)

## [1] TRUE

(x <- FALSE)

## [1] FALSE

class(x)

## [1] "logical"

Note: TRUE and FALSE must be written without quotation marks (they are logicals not characters).

Characters

The last atomic class we will deal with is the character class. A character is basically just a text and can be of any length.

(x <- "Austria")

## [1] "Austria"

(x <- "Max Konstantin Mustermann (AT)")

## [1] "Max Konstantin Mustermann (AT)"

class(x)

## [1] "character"

Checking class/type

As shown, class() and typeof() can be used to determine the class and type of an object. Both functions return a character vector which contains the name of the class/type (e.g., "numeric" or "integer").

Alternatively, a range of functions exist to check whether or not an object is of a specific type. These very handy functions return either a logical TRUE if the input is of this specific type, or FALSE if not. Examples are:

is.double()
is.numeric()
is.integer()
is.logical()
is.character()
is.vector()
… and many more.

Some examples:

is.integer(1.5)

## [1] FALSE

is.double(1.5)

## [1] TRUE

is.character("Bruno")

## [1] TRUE

is.vector(c(1, 2, 3, 4))

## [1] TRUE

These functions return to us one single logical value TRUE if the object is of a specific class/type, and a FALSE if not.

Double vs. numeric

Let’s make things a bit more complicated. If you are new to programming this might be a bit confusing. However, at some point it will get important to know that there is a small but important difference between “numeric” and “double”.

For those who already have a background in programming I would like to clarify the language. If you are coming from another programming language you might be familiar with objects of type “double”, “real”, “float”, and “integer”. A “double” is a double precision floating point numeric value (e.g., 0.001234). Depending on the programming language they might be referred to as “double”, “real”, or “float” which are basically the same. An “integer” is also a numeric value but from \(\pm \mathcal{N}_0\) ([..., -3, -2, -1, 0, 1, 2, 3, ...]; positive and negative natural numbers including zero). As we have learned, R is based on C and, thus, shares the data types “double” and “integer” with C. However, there is a difference between the class of an object in R and the type (which is the underlying type).

Let us check what class() and typeof() returns for 1, 1.0, and 1L:

Table 4.2: Difference between class and type.
x	class(x)	typeof(x)	is.double(x)	is.integer(x)	is.numeric(x)
`1`	numeric	double	TRUE	FALSE	TRUE
`1.0`	numeric	double	TRUE	FALSE	TRUE
`1L`	integer	integer	FALSE	TRUE	TRUE

The table shows (left to right) the value which is checked (x), the R class of the object x, the type of x, and three checks: whether the value x is double, numeric, or integer (is.*()).

1 and 1.0: are of class “numeric”. The underlying data type in C is “double”, thus both is.double() and is.numeric() return TRUE.
1L: this is how an integer is specified in R. 1L is of class “integer” and the underlying C type is also “integer”, however, an integer in R is also threated as “numeric”! Thus is.numeric() returns TRUE as well.

Why? Well, the philosophy is that one can use both for mathematical operations. In R there is no difference between 5L^2L, 5L^2.0, and 5.0^2L as in some other programming languages. Thus, is.numeric() basically tells us whether or not we can use this specific object (x) for mathematical calculations.

Keep this in mind, we may get back to it here and there, but we will not use the small but sometimes important difference between “double” and “numeric” often.

Missing values

One additional important element is the missing values. R knows two types of missing values: NaN and NA. NaN is “not a number” and results from mathematical operations which are illegal/invalid. NA on the other hand stands for ‘not available’ and indicates a missing value. NAs can occur in all the vectors discussed above, and keep their class.

NaN: Mathematically not defined (and always of class numeric).
NA: Missing value, NA’s still have classes!
NaN is also NA but not vice versa.

Example for NaN: Zero devided by zero (0 / 0) is not a valid mathematical operation, wherefore the result of the devision is NaN.

(x <- 0 / 0)

## [1] NaN

Let us check the class and see if the object x is ‘not a valid number’ (is.nan()) and/or a missing value (is.na()).

is.nan(x)    # Check if 'x' is NaN

## [1] TRUE

is.na(x)     # Check if 'x' is NA

## [1] TRUE

Note: Missing values in R still have a class. We can have missing numeric, integer, logical, or character missing values. They all look the same, but have a class attached to it.

class(x)  # The value from above

## [1] "numeric"

When defining a new object and storing a single missing value on it (with x <- NA), it will be ‘logical’ by default. We can, however, convert them (if needed).

# By default - logical
(x <- NA)

## [1] NA

class(x)

## [1] "logical"

# Convert to integer
(y <- as.integer(NA))

## [1] NA

class(y)

## [1] "integer"

# Convert to character
(z <- as.character(NA))

## [1] NA

class(z)

## [1] "character"

As show, all three objects (x, y, z) look identical and contain one missing value. However, the class of the three objects differs. More about missing values in the corresponding sections where they are getting important.

4.3 Creating vectors

Concatenating values `c()`

As quickly shown earlier, c() can be used to combine (one or) multiple elements to a new vector. An example:

(x <- c(1.5, 1000, 0.1))

## [1]    1.5 1000.0    0.1

This creates a numeric vector of length 3 with the three elements 1.5, 1000, and 0.1 (in this order).

Important: As mentioned at the very beginning of this chapter, vectors can only contain data of one type! We cannot easily mix e.g., a character string with numeric values or vice versa. It is possible, but we need to take care of what happens in this case. We will come back to that later (subsection Coercion (mixing objects)).

In the same way we can create vectors of other types, e.g., a character vector with three elements:

(y <- c("Austria", "Tyrol", "Innsbruck"))

## [1] "Austria"   "Tyrol"     "Innsbruck"

As each element (e.g., "Austria") itself can be seen as a character vector of length one, c() can also be seen (and used) to combine vectors just the same way as used for elements.

x <- c("Austria", "Tyrol", "Innsbruck")
y <- c("Germany", "Berlin", "Berlin")
z <- c(x, y)
z

## [1] "Austria"   "Tyrol"     "Innsbruck" "Germany"   "Berlin"    "Berlin"

length(z)

## [1] 6

We could, of course, repeat this example for all atomic vectors including doubles (numeric), logical, character, integer, and complex values (try it yourself!):

x <- c(0.5, 0.6, 0.7)            # double
x <- c(TRUE, FALSE, TRUE)        # logical
x <- c(T, F, T)                  # logical (!!!)
x <- c("a", "b", "c")            # character
x <- c(1L, 2L, 3L, 4L)           # integer
x <- 15:20                       # integer
x <- c(1+0i, 2+4i, 5+2i)         # complex

Warning: The example above shows that you could also use T and F as an abbreviation for TRUE and FALSE which you may see frequently when you ‘google’ something. Please don’t do that! T and F are not protected and can be changed. Below we re-define or overwrite T with "bar" and F with "FOO". Thus, c(T, T, F, T) becomes something completely different. Even worse: Imagine what happens if I re-define T <- FALSE and F <- TRUE.

c(T, T, F, T)

## [1]  TRUE  TRUE FALSE  TRUE

T <- "foo"        # overwrite T
F <- "bar"        # overwrite F
c(T, T, F, T)

## [1] "foo" "foo" "bar" "foo"

Thus, get used to TRUE and FALSE from the beginning. T and F are shorter, but you might run into strange problems at some point which can be avoided by just not using these abbreviations.

Function `vector()`

An alternative way to create a vector of a specific type and length is the function vector(). vector() requires two input arguments, namely the type of the vector (or ‘mode’) and the length of the vector.

# Double (numeric) vector of length 5
vector("double", length = 5)

## [1] 0 0 0 0 0

# Character vector of length 3
vector("character", length = 3)

## [1] "" "" ""

As you can see both vectors are empty. The default value of numeric vectors is 0, the default for character vectors is "" (just an empty character string, a text without any characters in it), and FALSE for logical vectors.

Numeric sequences

Regular sequences can be created using the function seq() and its shortcuts seq.int(), seq_along(), and seq_len().

Sequences: sequences are a set of numeric or integer values between two well defined points (from and to) with an equidistant spacing. By default the spacing/increment is 1L but can be explicitly specified using the by argument.
Repeat: Repeat allows to repeat a number (or a set of numbers) in different ways. We can repeat one element several times, repeat a vector multiple times, or repeat the elements of a vector multiple times.

Numeric sequences: We can create numeric sequences using the seq() (generic function) or seq.int() (internal/primitive function). You can try it out yourself, seq() and seq.int() would do the very same in the examples below. Some times it can be beneficial to use seq.int() as it might be much faster, but a bit less flexible. To create a sequence, we have to at least specify three input arguments:

from: Where to start the sequence.
to: Where to end the sequence.
length or by: either define the length of the resulting vector, or the increment by which the values change. Note: if to is less than from, by must be negative (decreasing sequence). Else you’ll get an error.

# Equidistant numeric sequence
seq(from = 1.5, to = 2.5, length.out = 5)  # Specify length

## [1] 1.50 1.75 2.00 2.25 2.50

seq(from = 4, to = -4, by = -0.5)          # Specify increment/interval

##  [1]  4.0  3.5  3.0  2.5  2.0  1.5  1.0  0.5  0.0 -0.5 -1.0 -1.5 -2.0 -2.5 -3.0
## [16] -3.5 -4.0

Technically, seq() can also be used to create integer sequences. However, this only works if all three arguments from, to, and by (default is 1L) are given, and all are integers!

# Explicitly define from/to/by as integers
(x <- seq(from = 10L, to = 100L, by = 10L))

##  [1]  10  20  30  40  50  60  70  80  90 100

class(x)

## [1] "integer"

# 'from' defined as a numeric value (10.0)
(y <- seq(from = 10, to = 100L, by = 10L))

##  [1]  10  20  30  40  50  60  70  80  90 100

class(y)

## [1] "numeric"

Thus, in practice, you should never rely on the class of the sequence returned by seq().

Integer sequences: There are three distinct functions to create proper integer sequences.

<from>:<to>: Two values separated by a colon (:); creates sequences in steps of +1 or -1. If <from> is an integer (or a numeric value without decimals), an integer sequence will be created.
seq_along(x): Creates a sequence from 1L to length(x) where x is an existing object (e.g., a vector).
seq_len(n): creates a sequence between 1L and n.

Two examples for <from>:<to>:

# Sequence from 1:4
(x <- 1:4)

## [1] 1 2 3 4

class(x)

## [1] "integer"

# Sequence from 30:25 (decreasing)
(y <- 30:25)

## [1] 30 29 28 27 26 25

class(y)

## [1] "integer"

To be able to use seq_along() we need an object along which we would like to create the integer sequence. Let us assume we have a character vector cities (see below), seq_along() will return a sequence counting from 1 up to the number of elements in names.

# Create character vector 'cities'
cities <- c("Vienna", "Paris", "Berlin", "Rome", "Bern")
seq_along(cities)

## [1] 1 2 3 4 5

Last but not least, seq_len() simply creates an integer sequence from 1L to n:

seq_len(10)

##  [1]  1  2  3  4  5  6  7  8  9 10

Character Sequences: If you need the letters of the alphabet, there are two convenient vectors which are available globally called LETTERS and letters. LETTERS contains the alphabet (no special characters) in upper case letters ("A", "B", …), letters the same in lower case letters ("a", "b", …). This can be used if one just wants to have some random character values.

# First 7 letters of the alphabet
LETTERS[1:7]

## [1] "A" "B" "C" "D" "E" "F" "G"

letters[1:7]

## [1] "a" "b" "c" "d" "e" "f" "g"

This is often a nice-to-have when one needs the first few letters of the alphabet or requires random characters in the code and will be used every now and then in this book.

Replicating elements

Another often useful function is replicate. Replicate can be used for all vectors, no matter if they are numeric, integer, character, or logical. The rep() function can be used in different ways:

Replicate one specific value n times.
Given an existing vector: Replicate each element n times.
Given an existing vector: Replicate the entire vector n times.
Given an existing vector: Replicate the elements different amount of times.

Let us start with the most simple case and replicate the value 2L five times:

rep(2L, 5)                # Case (1)

## [1] 2 2 2 2 2

For all other cases we need an existing vector. Let us use a variant of the character vector cities and do both: repeat each element three times, or repeat the entire vector three times.

cities <- c("Vienna", "Bern", "Rome")
rep(cities, each = 3)     # Case (2)

## [1] "Vienna" "Vienna" "Vienna" "Bern"   "Bern"   "Bern"   "Rome"   "Rome"  
## [9] "Rome"

rep(cities, times = 3)    # Case (3)

## [1] "Vienna" "Bern"   "Rome"   "Vienna" "Bern"   "Rome"   "Vienna" "Bern"  
## [9] "Rome"

Alternatively we can specify which element in the original vector (cities) should be replicated how often.

rep(cities, times = c(3, 2, 5))

##  [1] "Vienna" "Vienna" "Vienna" "Bern"   "Bern"   "Rome"   "Rome"   "Rome"  
##  [9] "Rome"   "Rome"

As you can see, the first element of cities is replicated three times, the second twice, and the last one five times.

Similar as for seq() there are some shortcuts, namely rep.int() and rep_len(). rep.int() is again the primitive (and sometimes much faster) version of rep(). rep_len() can sometimes be very handy. What it does is to:

Replicate elements of an existing vector until a specific length is reached.

Let us assume we would like to replicate the elements c(4, 5, 6) as often as necessary to get a vector of length 5, or 9:

rep_len(c(4, 5, 6), length.out = 5)    # Resulting vector has length 5

## [1] 4 5 6 4 5

rep_len(c(4, 5, 6), length.out = 9)    # Resulting vector has length 9

## [1] 4 5 6 4 5 6 4 5 6

It repeats the elements (always from left to right) until the new vector reaches the length specified as second input argument.

4.4 Coercion (mixing objects)

As mentioned in the first part of this section: Vectors can only contain elements of one type! Thus, if we combine elements of different types (e.g., combine a numeric value and character values as in the next example), R has to convert all elements into the same type/class as vectors can only contain elements of one type.

This is called ‘coercion’. We have to differ between implicit coercion (R chooses the best option) and explicit coercion (we force something to be of a different type).

Numeric and character

What happens if we try to mix elements of different classes, like numeric values and characters as in this example?

# Numeric and character = character
(x <- c(1.7, "1", "A"))

## [1] "1.7" "1"   "A"

class(x)

## [1] "character"

The object x is of class "character". This is one example of implicit coercion, and R decided that the best way is to convert all elements into character to lose as little information as possible.

In this case, 1.7 (numeric) can easily be converted into the character "1.7" (character), but we can’t easily convert "1" and "A" into numeric values. While it would work for "1" (numerically 1.0) the character "A" cannot be converted into a numeric value at all.

Note: The entire object x is now a character object. This is important as we can no longer use it for e.g., mathematical operations.

# What is x (character vector) times 5.0 (numeric)?
x * 5.0

## Error in x * 5: non-numeric argument to binary operator

Numeric and logical

Similar when mixing logical and numeric values. Again, R needs to bring all values to the same type and tries to lose as little information as possible. What we need to know here:

Every numeric value equal to 0/0L converted to logical results in FALSE.
Every numeric value not equal to 0/0L converted to logical results in TRUE.
Every TRUE converted to numeric will be 1 (or 1L).
Every FALSE converted to numeric will be 0 (or 0L).

Let us assume we have a logical FALSE and two numeric values 5.5 and 10.0 we could:

Option A: Convert FALSE into 0.0 and keep the other two values as they are.
Option B: Keep FALSE as it is and convert both (5.5, 10.0) to TRUE.

In the first case we only lose little information, in the second one we completely lose the original values of 5.5 and 10.0. Thus, we expect R to convert everything to numeric (not to logical). Let us try:

# Combine TRUE, 5.5, and 10.0.
(x <- c(FALSE, 5.5, 10.0))

## [1]  0.0  5.5 10.0

class(x)

## [1] "numeric"

Et voilà!

Explicit coercion

As mentioned in the beginning, we can also perform explicit coercion where we as users decide in which type/class the data should be converted.

A range of as.*() functions allows us to explicitly convert values between different classes. E.g., as.character(1.42) will convert the numeric value 1.42 into a character "1.42". A wide range of different as.*() functions exist such as:

as.integer()
as.numeric()
as.character()
as.logical()
as.matrix()
…

Let us create a new integer vector between 0 and 4, assign it to x, and convert this integer vector to character and logical:

# let `x` be an integer vector
# with elements 0, 1, 2, 3, 4.
(x <- 0:4)

## [1] 0 1 2 3 4

# Coerce to character
as.character(x)

## [1] "0" "1" "2" "3" "4"

# Coerce to logical
as.logical(x)

## [1] FALSE  TRUE  TRUE  TRUE  TRUE

As mentioned previously: In the coercion to logical all numeric values 0 will be converted to FALSE and all others (including negative values) to TRUE. Even if we use explicit coercion, it is sometimes not possible to convert from one class to another. Characters from the alphabet, such as "a" or "b" cannot be converted to numerics or integers. However, characters which are basically only characters containing a numeric value (e.g., "100", "135.3") can be coerced.

Missing values

If R is not able to convert elements, it will return NA (and throw a warning):

# let `x` be a character vector
(x <- c("a", "b", "c", "d"))

## [1] "a" "b" "c" "d"

# Coerce to integer
as.integer(x)

## Warning: NAs introduced by coercion

## [1] NA NA NA NA

# But ...
x <- c("1", "100", "a", "b", "33")
as.integer(x)

## Warning: NAs introduced by coercion

## [1]   1 100  NA  NA  33

Coercion summary

The following table contains a summary of what will happen if you convert the element x into one of the four classes “numeric”, “integer”, “logical”, or “character”:

x	as.numeric	as.integer	as.logical	as.character
2.9	2.9	2L	TRUE	“2.9”
0	0	0L	FALSE	“0”
4L	4	4L	TRUE	“4”
0L	0	0L	FALSE	“0”
TRUE	1	1L	TRUE	“TRUE”
FALSE	0	0L	FALSE	“FALSE”
“A”	NA	NA	NA	“A”
“TRUE”	NA	NA	TRUE	“TRUE”
“FALSE”	NA	NA	FALSE	“FALSE”
NA	NA	NA	NA	NA

Exercise 4.1 In the example above (Numeric and logical) we have seen that R converts c(FALSE, 5.5, 10.0) into a numeric vector. Use the same example and use explicit coercion to convert the vector into a logical vector (as.logical()).

What is the result? Check class.
Can you explain why the result is as it is?

Solution. We can do this in one step or two steps. Both yield the same result, of course. Two-step approach:

Two-line approach: We first create a new object x by combining the three elements. Note: In this case, implicit coercion is used and x will be a numeric vector (as in the example above). We then convert this vector into a logical vector by explicitly calling as.logical(x).

(x <- c(FALSE, 5.5, 10.0))

## [1]  0.0  5.5 10.0

(x <- as.logical(x))        # Overwrite 'x'

## [1] FALSE  TRUE  TRUE

class(x)

## [1] "logical"

One-line approach: We could, of course, also define the vector inside the as.logical() function call. R does the very same, except that we do not explicitly store c(FALSE, 5.5, 10.0), but directly forward it to the as.logical() function call.

(x <- as.logical(c(FALSE, 5.5, 10.0)))

## [1] FALSE  TRUE  TRUE

class(x)

## [1] "logical"

Result: The result is c(FALSE, TRUE, TRUE), a vector of class logical. What happens is the following:

c(FALSE, 5.5, 10.0) is implicitly converted to the numeric vector c(0, 5.5, 10.0).
We then use explicit coercion and convert c(0, 5.5, 10.0) into a logical vector.
As we know, each numerical value 0 is treated as FALSE and all numeric values not equal to 0 as TRUE.

Thus, we get FALSE for the first element, and TRUE for the second and third which gives the result c(FALSE, TRUE, TRUE).

4.5 Mathematical operations

Once we have a vector (even vectors of length 1; single value) we can perform arithmetic operations on them. A list of available arithmetic operators can be found on the help page ?Arithmetic. The following ones are available:

operator	description	example
+	addition	5 + 5 = 10
-	subtraction	5 - 5 = 0
*	multiplication	2 * 8 = 16
/	division	100 / 10 = 10
^ (or **)	exponent/power	5^2 = 25
%%	modulo	100 %% 15 = 10
%/%	integer division	100 %/% 15 = 6

While the first five should be well know, the latter two are often useful but might require some additional information.

Integer division: The result of the integer division 100 %/% 15 is 6 because 15 fits into 100 six times (15 * 6 = 90).
Modulo: The modulo/mod of 100 %% 15 is 10 as we can fit 15 six times in 100 (6 * 15 = 90), and the remaining is 10 (100 - 90 = 10). This can be very handy to check if a number is divisible. E.g., 100 %% 10 = 0 as 10 * 10 = 100, rest 0.

Beside mathematical operators (see table above) a series of relational and logical operators exist. The table above shows the most important operators (see also ?Comparison, ?Logic and ?match).

Type	Operator	Condition
Relational	`x < y`	Where `x` less than `y`
	`x > y`	Where `x` greater than `y`
	`x <= y`	Where `x` less than or equal to `y`
	`x >= y`	Where `x` greater than or equal to `y`
	`x == y`	Where `x` (exactly) equals `y`
	`x != y`	Where `x` is not equal to `y`
Logical	`!`	Negation (NOT; `!x == 20`, same as `x != 20`)
	`&`	Logical “and” (`x >= 20 & x < 35`)
	`\|`	Logical “or” (`x == 20 \| x > 45`)
	`xor`	Logical “exclusive or” (`xor(x == 20, x == 50)`)
Value matching	`x %in% y`	Where `x` is in `y` (value matching; character)
	`! x %in% y`	Where `x` is not in `y` (value matching; character)

To briefly demonstrate what relational operators are used for: Let us assume we have an integer vector x and we want to check (i) which element is identical to 100L, or (ii) which of the elements is less than or equal to 30L.

x <- c(30L, 100L, 120L, 10L, -30L, 50L)
x == 100L            # Which element in 'x' is equal to 100L

## [1] FALSE  TRUE FALSE FALSE FALSE FALSE

x <= 30L             # Which element in 'x' is less than or equal to 30L

## [1]  TRUE FALSE FALSE  TRUE  TRUE FALSE

Logical operators are used to combine multiple relational comparisons. For example, which elements in x are less than or equal to 30L or exactly 100L.

x <= 30L | x == 100L

## [1]  TRUE  TRUE FALSE  TRUE  TRUE FALSE

The result of relational or logical comparisons are always logical vectors and will become very useful to find/extract specific values, or to add logic to a program. We will discuss them in more detail and how to use them later (e.g., in Subsetting vectors, or Conditional Execution).

Vectors and scalars

We can use all the arithmetics on numeric vectors. E.g., multiply a sequence (1:10) with a scalar (a single number; e.g., 2):

# Multiply a sequence by 2
x <- 1:10
x * 2

##  [1]  2  4  6  8 10 12 14 16 18 20

Note that the operation is applied element-by-element. Each element of the vector is multiplied by 2. The same is true for all operators. Another example: given a sequence of numbers on x: which ones are divisible by 10?

# Our vector x
x <- c(43, 100, 34, 483, 1000)
x %% 10

## [1] 3 0 4 3 0

All elements where the modulo is 0 (rest 0, see above) are divisible by 10.

Vectors and Vectors (Matching Length)

We can also use arithmetics between two vectors. Let’s start with two vectors of the same length. Let x and y contain a set of three numeric values which we would like to add up.

# Our data
x <- c(500, 400, 600)
y <- c(10, 5, 100)
# Call x + y (addition) and x / y (division)
x + y

## [1] 510 405 700

x / y

## [1] 50 80  6

Both vectors (x and y) are of the same length. In this case, the operation is applied on pairs of elements; i.e., the first of x is added to the first element of y, the second element of x to the second element in y and so forth and so on. The same is true for the division, of course.

Vectors and vectors (non-matching lengths)

What if the length of the two vectors differ? Well, let’s see. x and y again contain some numeric values. However, the length of x is \(4\) while the length of y is only \(2\).

# Our data
x <- c(500, 400, 600, 800)
y <- c(100, 2)
# Call x + y (addition) and x / y (division)
x + y

## [1] 600 402 700 802

x / y

## [1]   5 200   6 400

In these situations, R recycles the shorter vector! Internally, R expands the vector y to c(100, 2, 100, 2). Thus,

in case of x + y the result is x + c(100, 2, 100, 2)
in case of x / y the result is x / c(100, 2, 100, 2)

This only works well if the length of one vector is a multiple of the length of the other one. If you try multiplying c(1, 1, 1) * c(5, 2), R will calculate c(1, 1, 1) * c(5, 2, 5) but will raise a warning message that the longer object length (here \(3\)) is not a multiple of the shorter object length (here \(2\)).

Logical values

Arithmetic operations can also be performed on logical elements. As we have just learned TRUE will always be converted to 1L, FALSE always to 0L. Thus, if we multiply c(TRUE, FALSE) by a factor of 100L R will return the result of c(1L, 0L) * 100L:

c(TRUE, FALSE) * 100L

## [1] 100   0

c(TRUE, FALSE) / 2

## [1] 0.5 0.0

This is not something one will use often, but can sometimes be useful.

Missing values

What if we perform arithmetic operations on missing values? All operations involving a missing value (NA) will always result in a missing value.

c(1, 2, NA, NA) * 100

## [1] 100 200  NA  NA

c(1, 2, 3, 4) * NA

## [1] NA NA NA NA

100 %% NA

## [1] NA

4.6 Vector attributes

All objects in R can have additional so called attributes. Attributes are used to store additional meta-information. They are not part of the data itself, but part of the object, and are used for building more complex objects on top of vectors. Examples for such ‘more complex’ objects are matrices, data frames, factors, or date/time objects as we will see in the upcoming chapters.

Typical examples of attributes are:

The class of the object.
The dimension of matrices or arrays.
Names of elements (vectors) or dimensions (matrices, arrays).

While some of the attributes are mandatory, others are optional. As we have seen previously, the function class() returns the class of the object. The class is a mandatory attribute and every object will always have a class and a length.

Beside the class, additional attributes can exist. To see if an object has such attributes we can use the function attributes() which extracts all attributes (except class).

Let us first define a plain atomic vector without any additional attributes.

# Plain vector
(x <- c(54, 1.82))

## [1] 54.00  1.82

attributes(x)

## NULL

As shown, attributes(x) returns NULL. NULL is a reserved word for the null object in R, an empty object. NULL basically means “nothing or no information”. Our plain vector x does not have any additional attributes.

Named vectors

One additional attribute is names. Names can be used to name individual elements of a vector. To demonstrate what this implies, let us create a numeric vector with two named elements.

# Adding optional names
(y <- c(age = 54, height = 1.82))

##    age height 
##  54.00   1.82

The output looks different now. Both elements have an additional name (a character) which is linked to the corresponding numeric value. Calling attributes() now returns the information that the object has an additional names attribute.

attributes(y)

## $names
## [1] "age"    "height"

Technically, names are simply an optional attribute of an R object. However, it is one of the ‘standard’ attributes for which a special function called names() exist. The function names() can be used for both:

To get the names of an object.
To set or overwrite the names of an object.

Named vectors can often be useful as:

They are self-explanatory (each element is named).
We can access specific elements by name (shown later).

As shown earlier, we can explicitly declare the names when creating a new vector. Let us use the very same:

# Create a named vector
(x <- c(age = 54, height = 1.82))

##    age height 
##  54.00   1.82

If we now call names(x) we will get a character vector with the names of the elements:

# Get/extract the names
names(x)

## [1] "age"    "height"

names() can not only be used to get the names, it can also be used to set or overwrite the names of a vector. An example:

# Plain vector (without names)
(x <- c(1L, 2L, 3L))

## [1] 1 2 3

names(x)

## NULL

# Add names
names(x) <- c("first", "second", "third")
names(x)

## [1] "first"  "second" "third"

##  first second  third 
##      1      2      3

If we assign values to names(x) (with the sets operator <-) R will set names or overwrite existing names of x. Note: the vector of names on the right hand side has to contain the same number of elements as the vector on the left hand side.

In case a vector already has names and we set new ones, the existing ones will simply be overwritten.

# Change the names of 'x'
names(x) <- c("1st", "2nd", "3rd")
x

## 1st 2nd 3rd 
##   1   2   3

It is also possible to only assign names to some of the elements, or give multiple elements the same name. However, this is not recommended. An example:

x <- c(200, age = 54, height = 1.82, height = 182, 200, 300)
names(x)

## [1] ""       "age"    "height" "height" ""       ""

As shown, R gives all unnamed elements the name "" (an empty character string). Thus, we now have three elements in the vector called "" and two called "height" which can quickly result in confusion or problems.

4.7 Subsetting vectors

Creating vectors is one part of the game, the second part is to be able to get information from a vector. Accessing specific elements of a vector (or an object in general) is called subsetting. Vectors can be subsetted in different ways:

By index (position in the vector).
Based on logical vectors.
By name (if set).

Note: It is very important to understand this concept as it works similar/the same for all R objects.

Subsetting by index

As we have learned previously, function calls use round brackets (e.g., class(), length()). Subsetting uses squared brackets ([...] or [[...]]).

The simplest way of subsetting a vector is subsetting by index. An index is simply the position of a specific element in a vector. R always starts counting at 1 and we can access the first element by calling x[1] (“give me the 1st element of x”), or the fifth element by using x[5].

# Create a demo vector of length 5
(x <- c(10, 20, 0, 30, 50))

## [1] 10 20  0 30 50

x[1]          # Extract first element by index

## [1] 10

x[5]          # Fifth element

## [1] 50

If we need multiple elements at the same time, e.g., the first and the fifth, we can use a vector of indices as follows:

x[c(1, 5)]   # Get the first and fifth

## [1] 10 50

x[c(5, 1)]   # Or the fifth and first (different order)

## [1] 50 10

Similarly, we can use negative indexes to get all values except some specific ones. E.g., x[-1] gives “all but the first element of x”.

x[-1]         # all but first

## [1] 20  0 30 50

x[-5]         # all but fifth

## [1] 10 20  0 30

x[-c(1, 5)]   # all except first and fifth

## [1] 20  0 30

Out-of-range indexes: What if we try to access elements outside the vector? Our vector (x <- c(10, 20, 0, 30, 50)) only contains 5 elements. Let us subset the elements 4:7, or element 100:

x[4:7]

## [1] 30 50 NA NA

x[100]

## [1] NA

R returns a missing value (NA) for all elements which are not defined inside the vector and does not run into an error.

Last/first few elements: Let us imagine we are only interested in the first three or last three elements of the same vector x. We can do this using ‘subsetting by indices’ as follows:

x[1:3]          # First three elements (element 1 - 3)

## [1] 10 20  0

x[3:5]          # Last three elements (elements 3 - 5)

## [1]  0 30 50

There are convenience functions for that:

head(x, n = 3) extracts the first n elements (by default n = 6).
tail(x, n = 3) extracts the last n elements (by default n = 6).

head(x, n = 3)

## [1] 10 20  0

tail(x, n = 3)

## [1]  0 30 50

If the vector is shorter than n, R will return the entire vector (try head(x, n = 10) or tail(x)).

The two functions head() and tail() are generic functions and will also work for most more complex objects.

Subsetting by name

If we have named vectors we can make use of the names of the elements to access them. Let us use the following named vector:

x <- c(age = 35, height = 1.72, zipcode = 6020)

We are interested in the value for the element "age". Instead of using x[1L] we can now use x["age"] for subsetting:

x["age"]

## age 
##  35

Note: The argument inside the brackets has to be a character string. x[age] does something different - in this case R expects that there is an object called age. If not existing, you will get an error message:

x[age]

## Error: object 'age' not found

As for subsetting by indexes, we can also ask for multiple elements at the same time. However, negative subsetting (x[-"age"]) does not work.

x[c("age", "zipcode")]  # get both, "age" and "zipcode"

##     age zipcode 
##      35    6020

x[-"age"]               # Does not work, results in an error

## Error in -"age": invalid argument to unary operator

Advantage of subsetting by name: We do not have to care about the position of the element in the vector. Imagine the following: we have two objects called person1 and person2 with the same information as we have had above.

# Create the two named vectors
person1 <- c(age = 49, height = 1.84, zipcode = 5001)
person2 <- c(zipcode = 5040, age = 13, height = 1.52)

Imagine we ASSUME that the age is always the first element and use subsetting by index (pick the first element of both vectors):

cat("Person 1 is ", person1[1L], "years old.\n")

## Person 1 is  49 years old.

cat("Person 2 is ", person2[1L], "years old.\n")

## Person 2 is  5040 years old.

You can see the problem. Named vectors help one to avoid this issue as we do not have to deal with the position in the vector but just the name. Let’s do the same but use subsetting by name:

cat("Person 1 is ", person1["age"], "years old.\n")

## Person 1 is  49 years old.

cat("Person 2 is ", person2["age"], "years old.\n")

## Person 2 is  13 years old.

The function cat() (concatenate and print) can be used to create output to the R console. It can take up multiple elements separated by commas, combine them into a character string and print the result. The \n at the end indicates a line break, such that (after each print) a new line is started.

cat() is used to create nicely formatted output (see ?cat for details).

Subsetting by logical vectors

Alternatively, we can use a logical vector to subset vectors. Remember: logical vectors contain either TRUE or FALSE. In the context of subsetting it can be used to get all elements where the logical vector contains TRUE. An example:

x <- c(30, 10, 20, 0, 30, 50)
x[c(TRUE, TRUE, FALSE, FALSE, FALSE, FALSE)]

## [1] 30 10

As you can see we only get the first two elements, as only the first two elements of the logical vector contain TRUE. The two vectors (vector x to be subsetted and the logical vector) should be of the same length, else the logical vector will be recycled.

This is not often used as explicitly as shown above where we actually define a logical vector (c(TRUE, TRUE, ...)). Logical vectors are the result of binary comparisons.

As we have already seen in subchapter Mathematical operations R comes with a series of relational and logical operators. They now become very handy to subset vectors. Given the vector above, let us find all elements in x which are larger than 25.

x > 25          # Shows the result of the relational comparison

## [1]  TRUE FALSE FALSE FALSE  TRUE  TRUE

x[x > 25]       # Use 'x > 25' (logical vector) for subsetting

## [1] 30 30 50

Some more examples which you can try yourself given our vector x <- c(30, 10, 20, 0, 30, 50):

x[x == 30]: Elements in x where x is (exactly) equal to 30
x[x == 30 | x == 50]: Elements where x is either equal to 30 OR equal to 50.
x[x == 30 & x == 50]: Elements where x is equal to 30 AND 50 at the same time. The result should be an empty vector as this is not possible.
x[x >= 30 & x < 40]: All elements where x is larger than or equal to 30, but less than 40.
x[x < 30 & x > 40]: All elements where x is less than 30 AND larger than 40 at the same time. Again, impossible, the result should be an empty vector.

Such expressions can also be more complex and/or use data over different vectors. We can also store the logical vector onto a new object and use this object for subsetting. As an example, imagine we have two numeric vectors age and height with the age and height of some people.

age    <- c(  25,   53,   21,   50,   18,   63)
height <- c(1.73, 1.69, 1.83, 1.57, 1.91, 1.75)

We would like to get the age of those smaller than 1.8. In this case we first perform the relational comparison on the vector height. The result (a logical vector) is stored onto a new object res. In a second step we then use res to subset the age vector.

res <- height < 1.8
res

## [1]  TRUE  TRUE FALSE  TRUE FALSE  TRUE

age[res]

## [1] 25 53 50 63

We can, of course, do this in one line:

age[height < 1.8]

## [1] 25 53 50 63

Or extend the expression to get the age for those who are smaller than 1.8 and older than 50 years.

age[age > 50 & height < 1.8]

## [1] 53 63

Warning: Avoid using == for floating point arithmetic on double vectors. This can lead to unexpected results due to small imprecisions. An example:

(1.5 - 0.5) == 1

## [1] TRUE

(1.9 - 0.9) == 1

## [1] FALSE

Alternative: Better use the function all.equal(). The function checks if numeric values are equal (but not exactly equal) by allowing for a (very small) tolerance. For those interested what the tolerance is, check ?all.equal.

all.equal(1.9 - 0.9, 1)

## [1] TRUE

Further functions

Besides the relational and logical operators shown above, some more exist.

&&, ||: Like & (and) and | (or) but evaluate only first elements until results are determined.
isTRUE(), isFALSE(): Test for single non-missing TRUE or FALSE.

Take care: there is a distinct difference between &/| and the longer form &&/||. While & and | can be used on vectors (element-wise logical comparison), the longer form evaluates left to right examining only the first element of each vector. The evaluation proceeds only until the result is determined. While the long form can be very handy in some situations (e.g., conditional execution) we will mainly use the short form (&/|) in this course.

Index of `TRUE` elements

Often one is interested in where elements are stored which match an expression. Therefore we can use the function which(). which() returns the indices of the elements where the expression evaluated to TRUE.

x <- c(30, 10, 20, 0, 30, 50)
x >= 30

## [1]  TRUE FALSE FALSE FALSE  TRUE  TRUE

which(x >= 30)

## [1] 1 5 6

The expression x >= 30 is TRUE for the elements at position or index 1, 5, 6, which is exactly what which() returns.

Example: Find the position of the minimum and the maximum of the vector x.

min(x)                # The minimum

## [1] 0

x == min(x)           # Comparison

## [1] FALSE FALSE FALSE  TRUE FALSE FALSE

which(x == min(x))    # Index/position

## [1] 4

The same can be done to find the maximum.

max(x)                # The maximum

## [1] 50

x == max(x)           # Comparison

## [1] FALSE FALSE FALSE FALSE FALSE  TRUE

which(x == max(x))    # Index/position

## [1] 6

In addition, there are two functions which.min() and which.max() which are more reliable to find the minimum/maximum of floating point numbers. However, they only return the index of the very first occurrence of the minimum/maximum! Imagine the following vector z. The minimum is 0.5 which occurs twice, position 2 and 5. Now compare the different result of which(z == min(z)) and which.min(z):

z <- c(10, 0.5, 20, 30, 0.5)
which(z == min(z))     # Position/index of all minima

## [1] 2 5

which.min(z)           # Position/index of first occurrence of minimum

## [1] 2

The same is valid for which.max().

Single and double brackets

In the beginning of this chapter it was mentioned that we can use single brackets ([]) or double brackets ([[]]) for subsetting. While we will most often use single brackets, let us see what they do different.

[] keeps the name attribute, while [[]] drops them all. If we have an unnamed vector there is no difference between the two:

(x <- c(54, 1.82, 6020))

## [1]   54.00    1.82 6020.00

x[3]       # Single brackets

## [1] 6020

x[[3]]     # Double brackets

## [1] 6020

However, if we have a named vector the result of the two commands look different:

(x <- c("age" = 54, "height" = 1.82, "zipcode" = 6020))

##     age  height zipcode 
##   54.00    1.82 6020.00

x[3]

## zipcode 
##    6020

x[[3]]

## [1] 6020

The same is true for subsetting by name or logical vectors.

4.8 Vector functions

There are several functions which can be used to get information from vectors, manipulate vectors, or inspect vectors. This section highlights some useful ones, including:

Function	Description
`round()`	Round numeric values
`min()`, `max()`	Minimum and maximum
`mean()`, `median()`	Arithmetic mean and median
`sum()`	Sum
`sd()`, `var()`	Standard deviation and variance
`sqrt()`	Square root
`summary()`	Numerical summary
`str()`	Overview of the object structure
`any()`, `all()`	Test vector elements
`all.equal()`	Test for near equality
`sort()`	Sort a vector
`order()`	Obtain ordering of a vector

To demonstrate these functions, we will use pseudo-random numbers from a standard normal distribution which can be drawn using the function rnorm(). As random numbers are random (by definition) we would all get completely different numbers.

For the purpose of reproducibility we will call set.seed() to fix a random seed. Thus, we should all get the same random numbers. As they are no longer completely random, one calls them “pseudo-random”.

set.seed(6020)     # A specific seed; fixed using an integer
x <- rnorm(100)    # Draw 100 random numbers from the standard normal distribution
head(x, n = 10)    # Show first 10 elements

##  [1] -0.3421647  0.4528670  0.6169125 -0.6121245 -1.2603337 -0.4266803
##  [7] -1.7461032 -0.8736939  1.0627069  0.3600695

On your computer you should get the very same numbers as shown here (due to the seed we set).

Exercise 4.2 Understanding set.seed() and pseudo-randomization.

Set a random seed using set.seed(). Chose any integer number you like (e.g., set.seed(1)).
Draw 5 random values from the standard normal distribution using rnorm(5) and store the result on r1.
Set the very same seed again (as in step 1).
Draw another 5 random numbers (rnorm(5)) and store there result on r2.
Without setting the seed again, draw 5 more random numbers and store it on r3.

Now compare r1, r2, and r3. What do you observe?

Solution. r1 and r2 should contain the very same numbers due to the seed we set. The numbers are no longer purely random, but depend on the seed. This helps to make things reproducible as we always obtain the same numbers.

r3 however should have different values. As we have not set the seed again, we now get a different set of values.

# (1) Set a seed (using seed number 1 here).
set.seed(1)
# (2) Draw 5 random values.
r1 <- rnorm(5)
# (3) Set the very same seed again.
set.seed(1)
# (4) And draw another 5 random values.
r2 <- rnorm(5)
# (5) Draw 5 more random values without setting the seed.
r3 <- rnorm(5)
# Compare results
r1

## [1] -0.6264538  0.1836433 -0.8356286  1.5952808  0.3295078

r2

## [1] -0.6264538  0.1836433 -0.8356286  1.5952808  0.3295078

r3

## [1] -0.8204684  0.4874291  0.7383247  0.5757814 -0.3053884

We now use vector x from above to demonstrate what the functions above do. Let us start with round(). By default, round() rounds to 0 digits (closest natural number) which can be respecified using the additional argument digits.

head(round(x, digits = 1), n = 10)   # Round, show first 10 elements only

##  [1] -0.3  0.5  0.6 -0.6 -1.3 -0.4 -1.7 -0.9  1.1  0.4

We can also obtain/calculate the minimum, maximum, arithmetic mean, median, variance, standard deviation, the sum over all and the number of elements:

c(min  = min(x),     max    = max(x),
  mean = mean(x),    median = median(x),
  var  = var(x),     sd     = sd(x),
  sum  = sum(x),     length = length(x))

##           min           max          mean        median           var 
##  -2.342863490   2.654889032  -0.004146298   0.074796745   0.905993511 
##            sd           sum        length 
##   0.951836914  -0.414629842 100.000000000

Exercise 4.3 Using a bit of basic math we can show that:

The arithmetic mean is nothing else than the sum over all elements divided by the number of elements: \(\bar{x} = \frac{1}{n} \sum_{i=1}^N x_i\).
The standard deviation is the square root (sqrt()) of the variance \(\text{SD}(x) = \sqrt{\text{VAR}(x)}\).
The variance is the standard deviation squared: \(\text{VAR}(x) = \text{SD}(x)^2\).

Try to calculate the arithmetic mean using sum() and length() and compare the result to the result of mean(). Calculate the variance using sd(), and calculate the standard deviation using var(). Compare the results to the result of sd() and var(); all based on our vector x.

Solution. Arithmetic mean: To get the arithmetic mean we only have to sum up all elements of the vector x and divide it by the number of elements (the length of the vector):

mean(x)

## [1] -0.004146298

sum(x) / length(x)

## [1] -0.004146298

We can use the function all.equal() to compare if two numeric values are (nearly) equal and that our result is correct:

all.equal(mean(x),  sum(x) / length(x))

## [1] TRUE

Variance: We can use sd() to calculate the standard deviation and take it to the power of 2 (^2), or simply multiply sd() * sd() to get the same result.

all.equal(var(x), sd(x)^2)

## [1] TRUE

all.equal(var(x), sd(x) * sd(x))

## [1] TRUE

Standard deviation: As the variance is the standard deviation squared, the standard deviation must be the square root of the variance. The square root can be calculated using sqrt():

all.equal(sd(x),  sqrt(var(x)))

## [1] TRUE

Two more very important generic functions are str() and summary(). They are very helpful to get a first impression of the structure of an R object (str()) and its data (summary()).

str(x)     # Structure

##  num [1:100] -0.342 0.453 0.617 -0.612 -1.26 ...

str(x) tells us that our object x is a numeric (num) vector with elements \(1\) to \(100\) (1:100), the rest of the output shows us the first few elements of x.

summary(x) # Numerical summary

##      Min.   1st Qu.    Median      Mean   3rd Qu.      Max. 
## -2.342863 -0.590057  0.074797 -0.004146  0.648840  2.654889

The summary(x) function returns a numerical summary of the object. For numeric values, the summary consists of the minimum, 1st quartile, median, the mean, 3rd quartile, and the maximum of all elements in x. If the vector contains missing values (NA) the summary statistics would also tell us how many NAs we have in the vector.

Missing values

So far, our vector x contains no missing values. What if we have missing values (NA) in a vector? For demonstration, we create the very same vector again but add 5 missing values at position 2, 4, 50, 70, and 99.

# Generate the vector (again).
set.seed(6020)
x <- rnorm(100)
# Replace element 2, 4, 50, 70, and 99 with a missing value (NA)
x[c(2, 4, 50, 70, 99)] <- NA

If we now check the summary statistics we can see that it reports the number of missing values:

summary(x)

##      Min.   1st Qu.    Median      Mean   3rd Qu.      Max.      NA's 
## -2.342863 -0.573185  0.053709  0.003272  0.719625  2.654889         5

Let us check if the number of NAs reported by summary() is correct. Therefore we use is.na() which returns a logical vector with TRUE if a value is a missing value and FALSE else. As every TRUE counts as 1 and ever FALSE as 0 (numerically) we can simply sum up this vector.

# Count missing values
sum(is.na(x))

## [1] 5

We have 5 TRUEs and 95 FALSEs, thus the sum is 5 and (of course) the same as summary() returns.

Mathematical operations: as mentioned earlier all mathematical operations return NA as soon as at least one missing value is involved in the calculation. This is true for all functions shown below:

c(min  = min(x),     max    = max(x),
  mean = mean(x),    median = median(x),
  var  = var(x),     sd     = sd(x),
  sum  = sum(x))

##    min    max   mean median    var     sd    sum 
##     NA     NA     NA     NA     NA     NA     NA

How to handle missing values? There are basically two options on how we can handle this situation.

Think about where they come from. Is it a problem? Is it realistic to have missing values, do I understand why they are there? Can I ignore it or is the data set invalid and I have to go back ‘to the lab’?
Simply remove (delete) all NAs and ignore it.

The latter one is not the way to go! Whenever you encounter missing values in a data set: think about it. There are many situations where missing values are part of a data set and it is OK to have them included. All we have to do is to properly account for them. However, sometimes missing values indicate that your data set is invalid and you should not proceed as you may end up with false conclusions or results!

Once you know why it happens and that it is OK to use the data set we have two options:

Remove all missing values. This can be done using the na.omit() function. na.omit() simply removes missing values from the vector (you’ll end up with a shorter vector).
Keep the missing values and account for them using the na.rm option which is available for a wide range of functions.

Omit missing values: Omit all missing values in x, store the new vector (without missing values) on x2 and check it’s length.

x2 <- na.omit(x)
c(length(x), length(x2))

## [1] 100  95

As you can see, we dropped the five missing values from x. We can now use x2 to do our calculations (e.g., calculate the mean or the variance). Alternatively, we keep the missing values and account for them using the additional input argument na.rm = TRUE.

c(mean(x, na.rm = FALSE),   # Default
  mean(x, na.rm = TRUE))    # Account for missing values

## [1]          NA 0.003271709

This option exists for a wide range of functions:

# Minimum, maximum, mean, median, variance, and standard deviation
c(min  = min(x, na.rm = TRUE),     max    = max(x, na.rm = TRUE),
  mean = mean(x, na.rm = TRUE),    median = median(x, na.rm = TRUE),
  var  = var(x, na.rm = TRUE),     sd     = sd(x, na.rm = TRUE),
  sum  = sum(x, na.rm = TRUE))

##          min          max         mean       median          var           sd 
## -2.342863490  2.654889032  0.003271709  0.053709304  0.936059399  0.967501627 
##          sum 
##  0.310812328

`all()` and `any()`

These two functions check if either all elements match a certain condition (all), or at least one (any), based on logical vectors.

all() simply checks if all elements are TRUE. If so, a logical TRUE will be returned, otherwise FALSE is returned. Some examples:

# Are all elements TRUE?
all(c(TRUE, TRUE, TRUE))

## [1] TRUE

all(c(0L, 0L, 0L) == 0L)

## [1] TRUE

all(c(1, 2, 3, 4) > 2)

## [1] FALSE

any() does basically the same but returns TRUE as soon as at least one element is equal to TRUE.

# Is any element TRUE?
any(c(TRUE, FALSE, FALSE))

## [1] TRUE

any(c(0L, 0L, 0L) == 0L)

## [1] TRUE

any(c(-5, -3, -1) > 0)

## [1] FALSE

This can be very handy if we would like to check if we for example have any missing value in a vector. The function is.na() checks if a value is NA. This in combination with any() tells us if we have missing values.

x <- c(10, 30, 50, NA, NA, 30)
y <- c(10, 30, 50,  0, 50, 10)
any(is.na(x))

## [1] TRUE

any(is.na(y))

## [1] FALSE

4.9 Plotting vectors

Well, one key feature of R is it’s ability to graphically display data (plotting). Visualizing data in some sort or form can often be very helpful to better understand the data and/or identify possible problems such as outliers or unrealistic values. We (as humans) are very efficient in processing visual information, classify and cluster data, or identify certain patterns or structures on a plot - something which is nearly impossible by looking at dozen’s or hundreds of numeric values.

Base R comes with a range of plot types and plotting functions. In this chapter we will go trough the very basics of plotting vectors. Some more information about plotting can be found in the chapter Plotting in this book.

There are several different basic plot types, including:

Function	Description
`plot()`	Generic X-Y plot
`barplot()`	Bar plot
`pie()`	Pie chart
`hist()`	Histogram
`boxplot()`	Box-and-Whisker plot

These are all generic functions and will react differently for different objects. In this section we will focus on named and unnamed (plain) atomic vectors.

Generic X-Y Plot (Vector)

Creates a two-dimensional scatter plot. If only one input is given (the ‘x’) the values will be plotted against the y-axis, while the x-axis shows the index or position of the element in the vector. A simple example:

# Create the data vector
d <- c(10, 5, 30, 20, -5, 11)
plot(d)

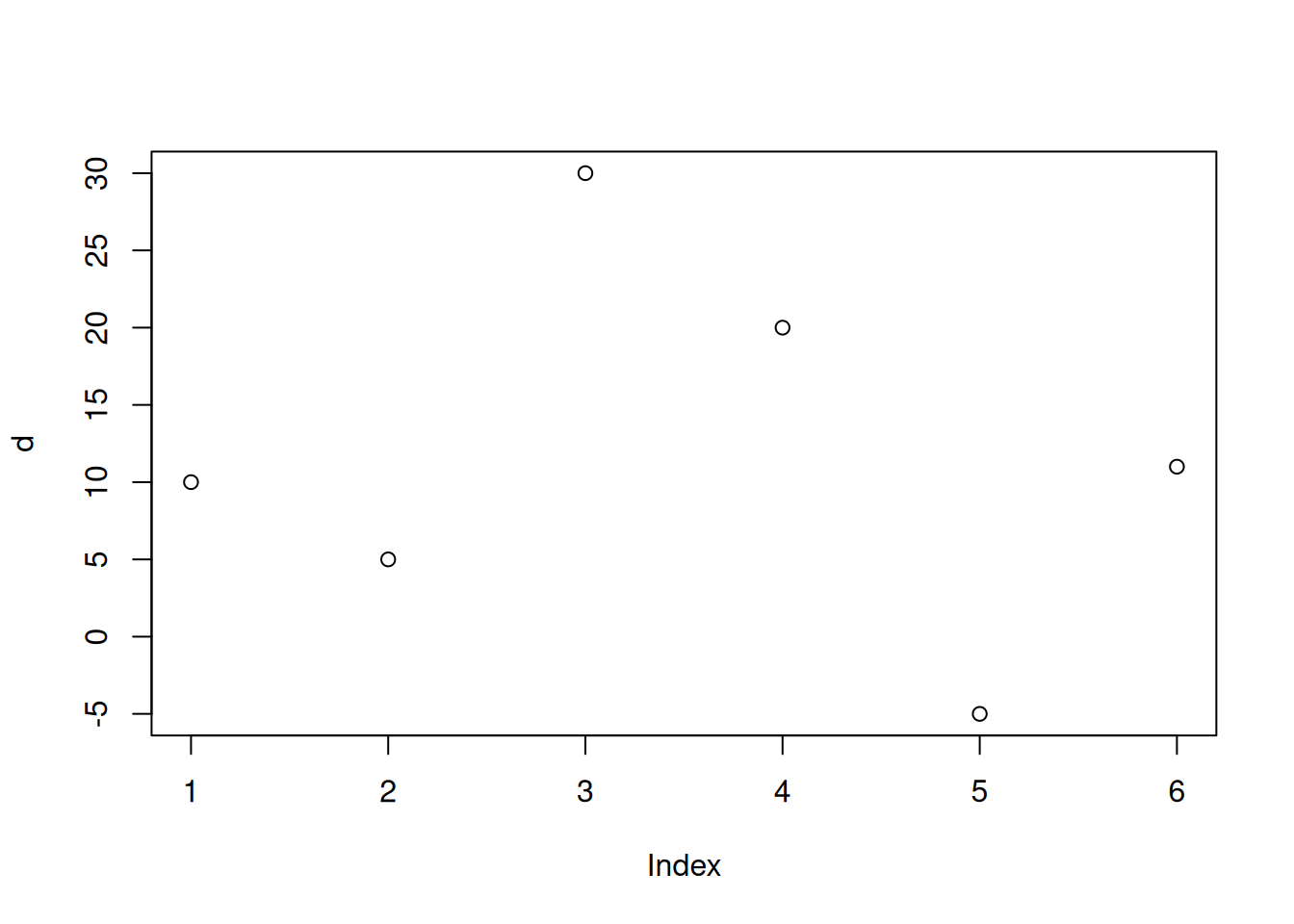
R automatically labels the axis according to what is shown - and the name of the object (here d). There are several options to enhance the plot such as setting a title, rename the axis, or adjusting the way the data are shown.

# Create the data vector
d <- c(10, 5, 30, 20, -5, 11)
plot(d,
     main = "Figure Title",
     xlab = "index/position in the vector",
     ylab = "measurement",
     type = "l", col = 4, lwd = 3)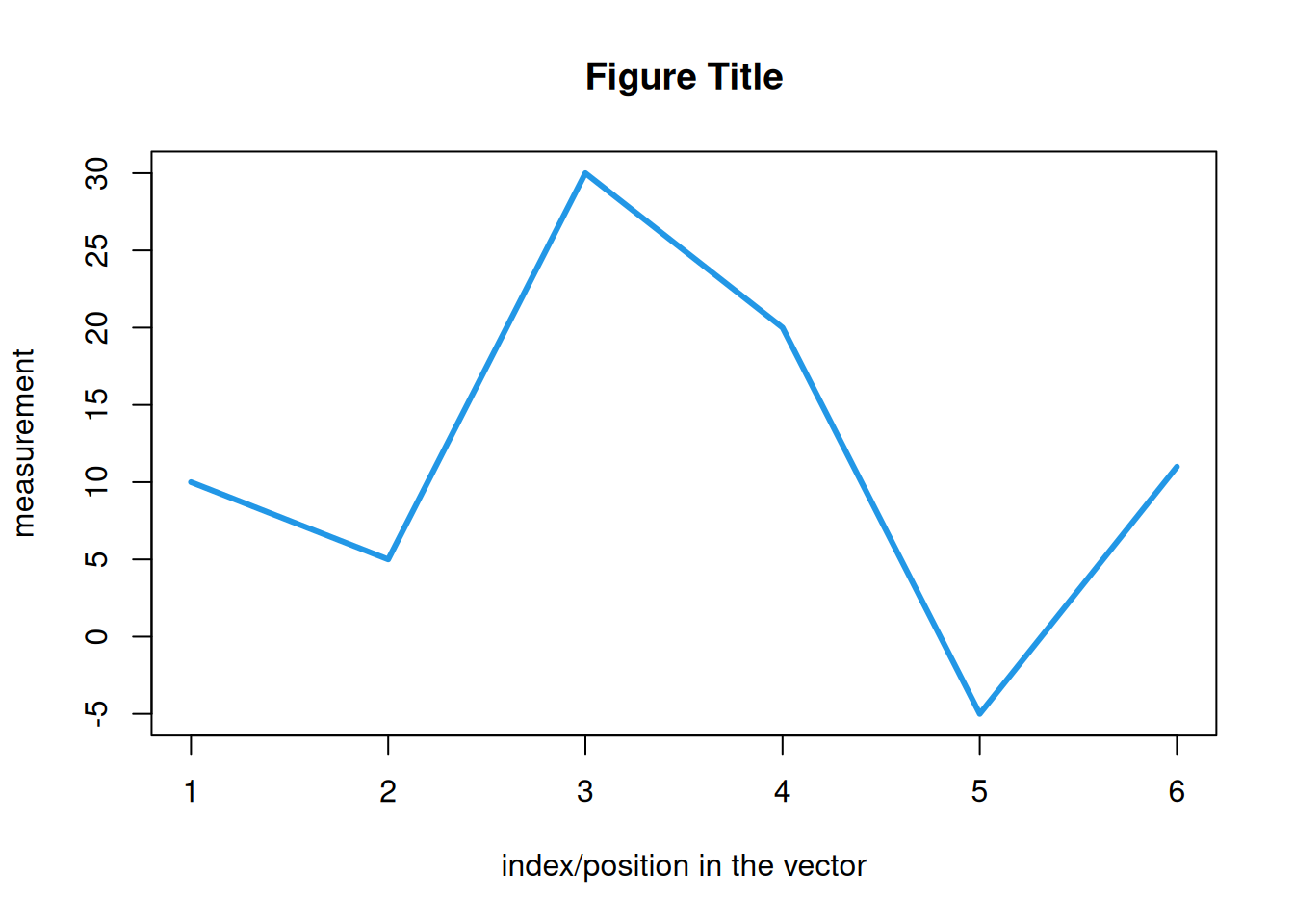

For more details check out the manual page ?plot and/or the Plotting chapter. We can also use it to plot two vectors (same length) against each other. The example below visualizes the sine function between \(-\pi\) and \(+\pi\).

# Sequence from -pi to pi (used for x-axis)
x     <- seq(-pi, pi, length.out = 501)
# Sine of 'x' evaluated for each element in 'x' (used for y-axis)
sinex <- sin(x)
plot(x, sinex, type = "l")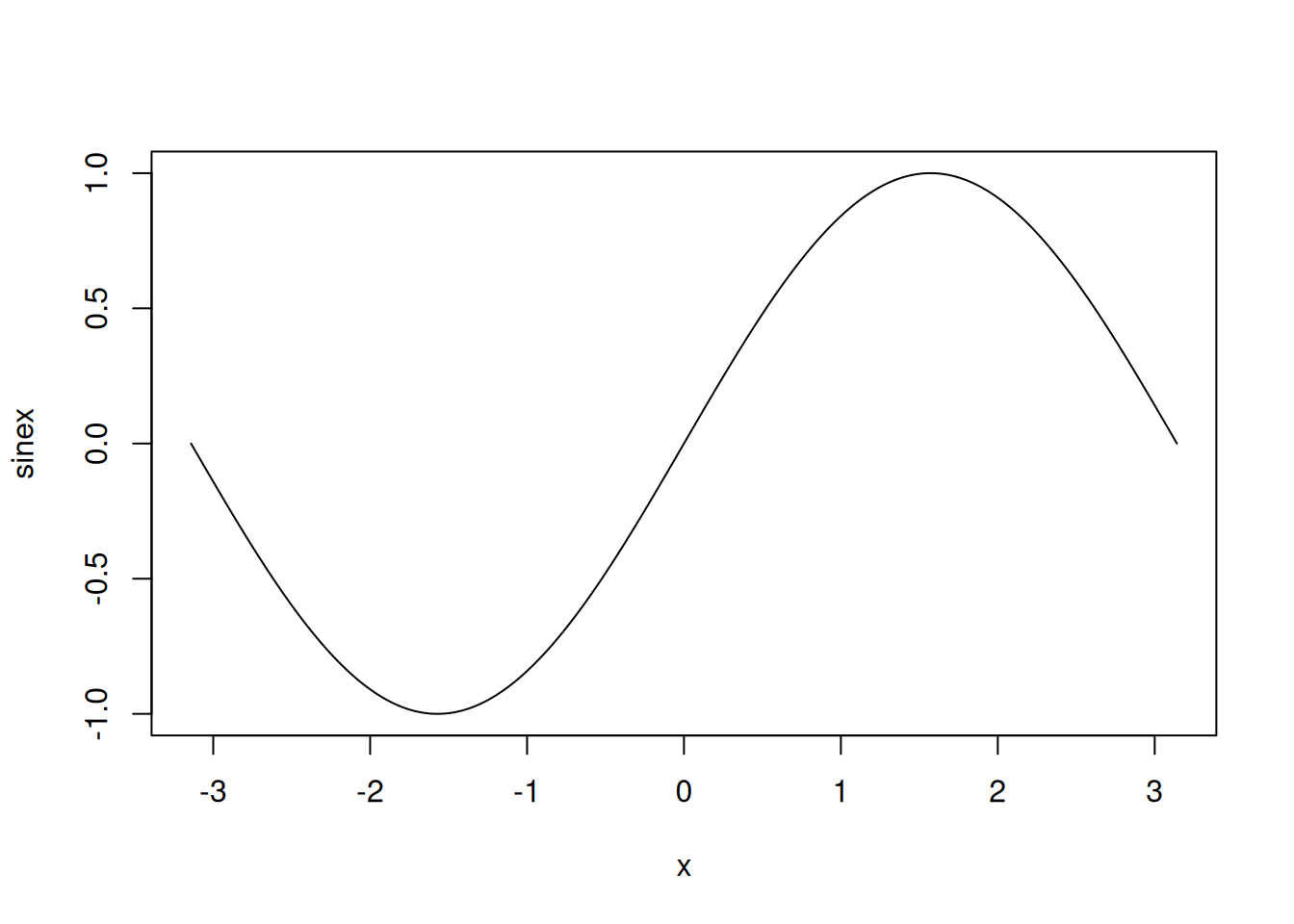

We can also plot functions in R using plot(<function name>). The function is then evaluated along the x-axis. Only works for functions taking up one value x as first input argument. By default, the function is evaluated between 0 and 1, however, we can specify this using custom x-limits.

plot(sin, xlim = c(-pi, pi), main = "Sine function", type = "l")

Other functions might be cos(), sqrt(), log(), … Feel free to try it yourself!

Bar plot

Bar plots are typically used to visualize data for specific groups or classes. Let us assume we would like to visualize the outcome of the latest Austrian legislative election from 2019 (Nationalratswahlen; source wikipedia) and plot the number of seats the parties got out of the election.

This is a classical example to use a named vector in combination with barplot().

election_results <- c("ÖVP"          = 71,
                      "SPÖ"          = 40,
                      "FPÖ"          = 30,
                      "Grüne"        = 26,
                      "NEOS"         = 15,
                      "Fraktionslos" = 1)
barplot(election_results)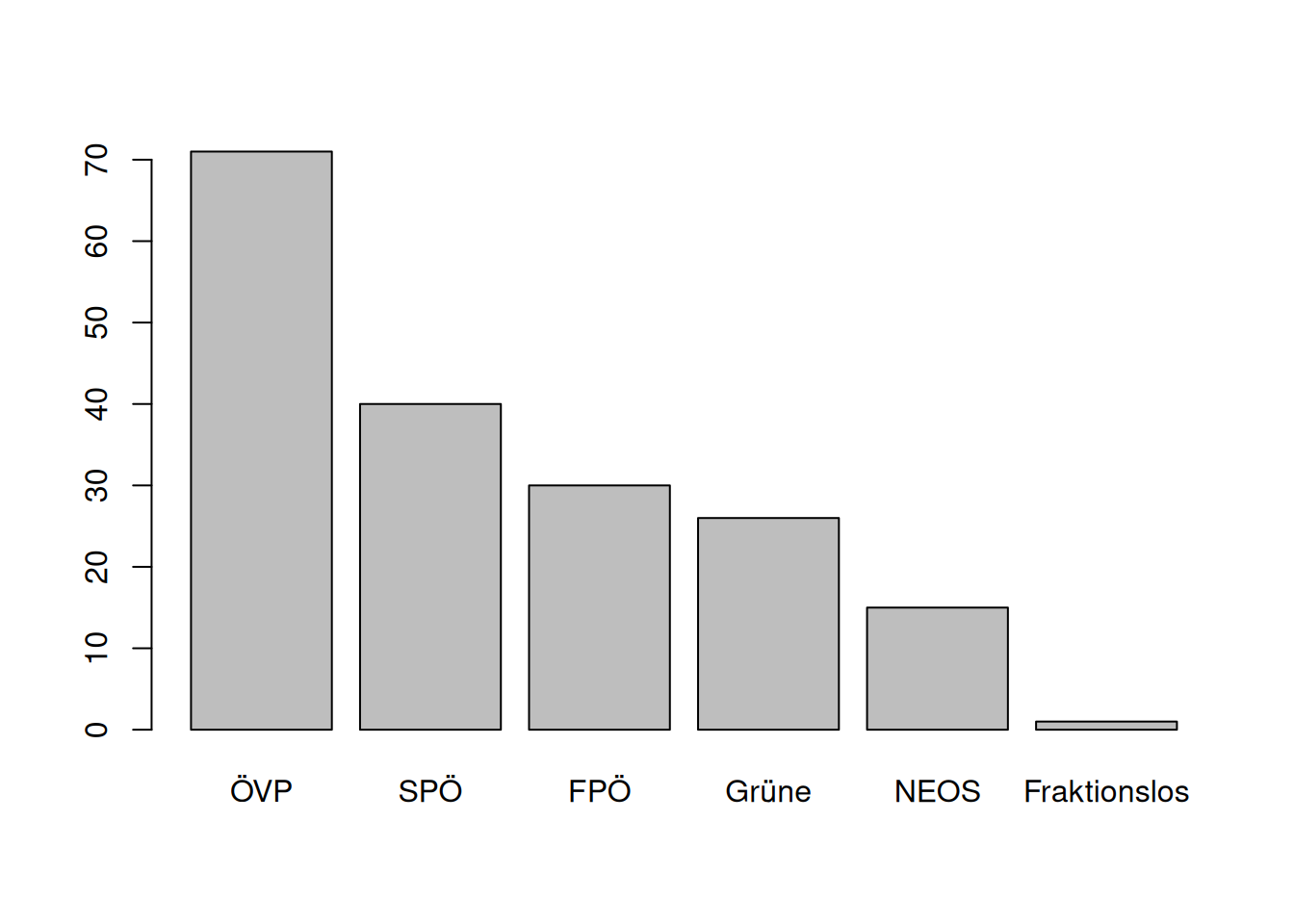

Again, we can modify the look and feel to our wishes:

barplot(election_results,
        main = "Resultat Nationalratswahlen 2019",
        xlab = "Kurzbezeichnung Partei",
        ylab = "Sitze",
        col  = c("turquoise3", "firebrick2", "dodgerblue3", "green4", "violetred2", "gray70"))

Pie plot

An alternative plot type are pie plots. Keep in mind that pie plots are often not the most effective way of visualizing data. However, if needed, we can do it as follows:

pyramid <- c("Sky" = 70,
             "Sunny side\nof pyramid" = 20,
             "Dark side\nof pyramid" = 10)
par(mar = rep(1, 4L)) # reduce border margin
pie(pyramid, init.angle = -35, col = c("#0099FF", "#FFE452", "#AA9526"),
    main = "Pie")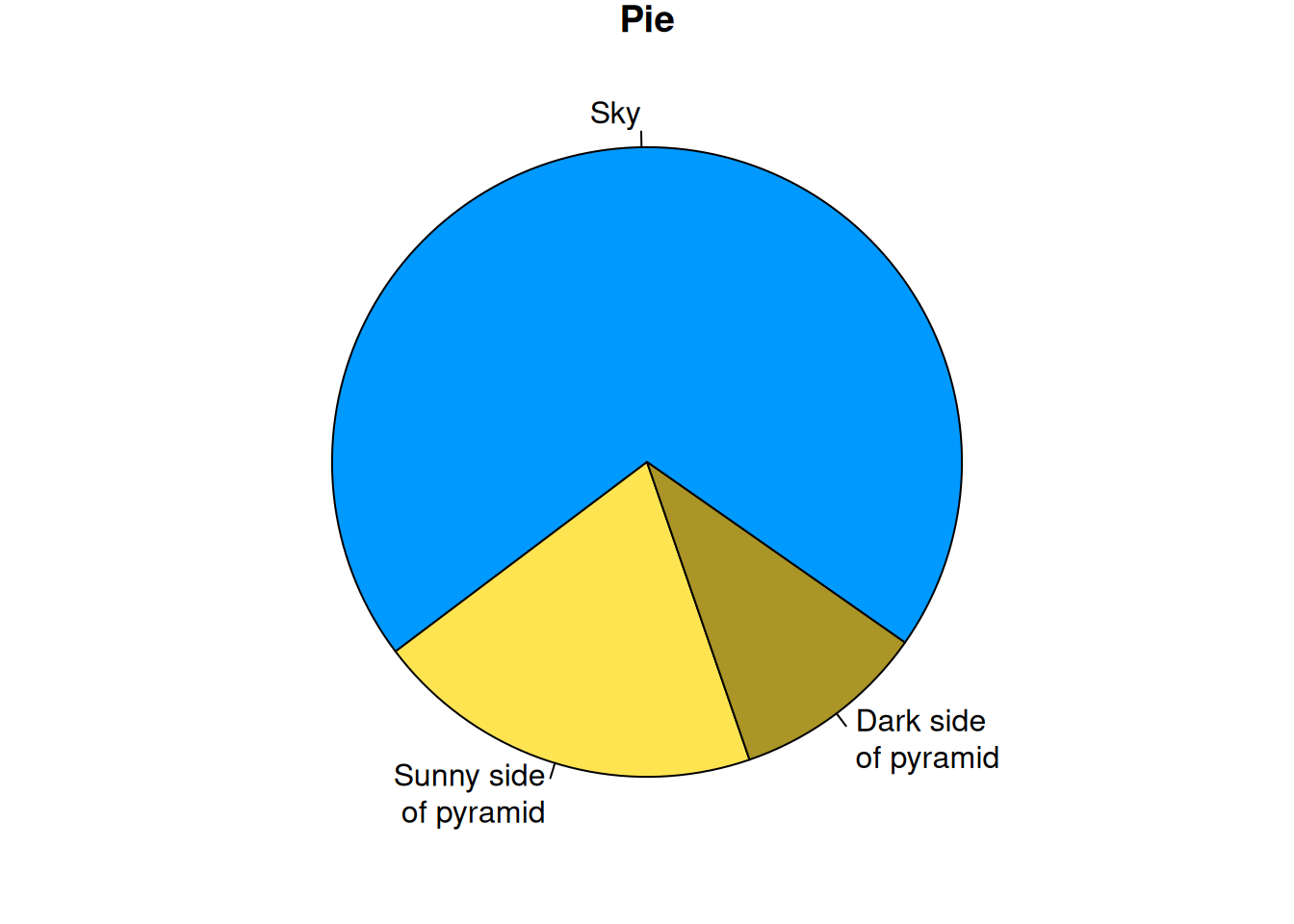

Again, if we have a named vector, R automatically takes the names to label the different sections of the pie (see ?pie for more customization options).

Histograms

A way to visualize large amounts of numeric values are histograms. Histograms show the distribution of the data. For demonstration, let us draw 1000 random values from a standard normal distribution (rnorm(1000)).

We can now see how they are distributed (should show a normal distribution centered around 0 with a variance/standard deviation of 1):

d <- rnorm(1000)
hist(d)

Another example: Mixing random values by drawing 1000 out of the standard normal distribution (with mean 0 and standard deviation 1) and 500 from a normal distribution with mean 7 and standard deviation 2:

d <- c(rnorm(1000, mean = 0, sd = 1),
       rnorm(500,  mean = 7, sd = 2))
hist(d,
     freq = FALSE,    # Show density instead of frequency
     breaks = 50)     # Number of breaks

Box-and-Whisker plot

An alternative way to show the distribution of numeric values are Box-and-Whisker plots.

x <- (5 + rnorm(100))^5 # Generate some values
boxplot(x)

summary(x)

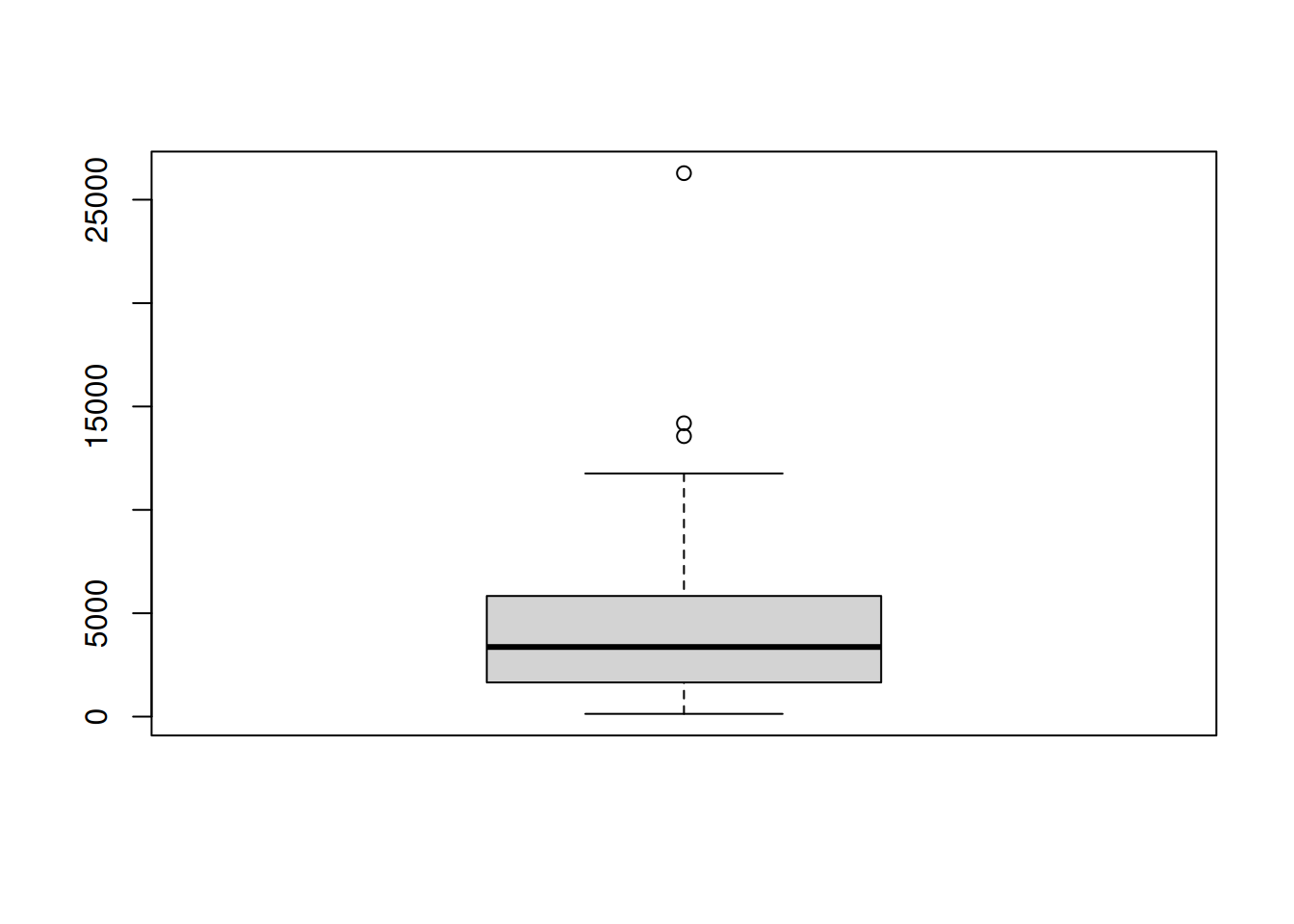
##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##   132.5  1668.0  3366.4  4240.6  5753.1 26284.2

The box (gray box) shows the 1st, 2nd (median) and 3rd quartile, the same as returned by summary(). The Whiskers (lines) show the data which lie within 1.5 times the inner quartile range from the box, while outliers (those being further away) are plotted as dots. The full range of the plot also shows the minimum/maximum of the data.

Box-and-Whisker plots are especially useful to compare data from different groups, something shown at a later time.

Interested in additional learning material about vector algebra? Or even participating in the course “198812 VU Computer Programming Prerequisites” by the DiSC? Feel free to have a look at these tutorials with vector algebra exercises and how to do it in R. This is optional material and not part of the R programming course!

Chapter 4 Vectors

4.1 Objects in R

Know the basics!

Print objects

4.2 (Atomic) vectors

Important vector functions

Double (or numeric)

Integers

Logical

Characters

Checking class/type

Double vs. numeric

Missing values

4.3 Creating vectors

Concatenating values c()

Function vector()

Numeric sequences

Replicating elements

4.4 Coercion (mixing objects)

Numeric and character

Numeric and logical

Explicit coercion

Missing values

Coercion summary

4.5 Mathematical operations

Vectors and scalars

Vectors and Vectors (Matching Length)

Vectors and vectors (non-matching lengths)

Logical values

Missing values

4.6 Vector attributes

Named vectors

4.7 Subsetting vectors

Subsetting by index

Subsetting by name

Subsetting by logical vectors

Further functions

Index of TRUE elements

Single and double brackets

4.8 Vector functions

Missing values

all() and any()

4.9 Plotting vectors

Generic X-Y Plot (Vector)

Bar plot

Pie plot

Histograms

Box-and-Whisker plot

Concatenating values `c()`

Function `vector()`

Index of `TRUE` elements

`all()` and `any()`