Chapter 14 Exploratory Data Analysis

As an addition to the main course material, let us have a look at exploratory data analysis and how we can easily create numerical and graphical summaries. One of the strenghts of R plotting which we will make use of to visualize the information of the “cod.xlsx” data set.

As shown in the previous chapter, we load and prepare our data set with the following lines of code, here put into a function called prepare_cod_data():

# Custom function
prepare_cod_data <- function(file) {
    # Input sanity check.
    # 'file' must be character, length 1, and file must exist
    stopifnot(is.character(file), length(file) == 1, file.exists(file))
    # Loading the required library
    require("readxl")
    # Import/read the data set, convert to data frame
    x <- data.frame(read_excel(file))
    # Transform variables
    x <- transform(x,
                   prevalence = as.logical(prevalence),
                   area       = as.factor(area),
                   sex        = factor(sex, 1:2, c("male", "female")))
    # Remove all observations with missing values and return data set
    return(na.omit(x))
}
 
# Loading the data set
cod <- prepare_cod_data("cod.xlsx")
head(cod, n = 3)
##    intensity prevalence   area year depth weight length    sex stage age
## 37         0      FALSE soroya 1999    51   1016     47 female     1   3
## 38         0      FALSE soroya 1999    51   1584     53   male     1   5
## 39         0      FALSE soroya 1999    51   1354     55   male     1   4

In the following: We will look at single variables and pairs of variables.

  • Exploratory analysis of a single numerical vs. categorical variable.
  • Exploratory analysis of pairs of variables.

Data

  • Numeric “response”: Fish weight and length.
  • Categorical “response”: Parasite prevalence (logical) and area (factor).

14.1 Single numeric

Numerical summary

Having numerical variables we have already seen a series of functions to investigate the values. This includes:

  • Tukey’s five-number summary() and sample mean.
  • Standalone functions: mean(), median(), min(), max(), and fivenum().
  • Arbitrary quantiles: quantile().
  • Measures of spread: Variance var(), standard deviation sd(), inter-quartile range via IQR().
summary(cod$weight)
##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##      38     798    1467    1741    2239    9990
c(variance = var(cod$weight), standard_deviation = sd(cod$weight))
##           variance standard_deviation 
##        1858879.920           1363.407

Calculate the quantiles \(0.3333\), \(0.6666\) (\(1/3\), \(2/3\)).

quantile(cod$weight, probs = c(1/3, 2/3))
## 33.33333% 66.66667% 
##      1034      1942

Which tells us that one third of all fishes weight less than 1034, one third of all fished betweeen 1034 and 1942, and one third more than 1942.

Graphical summary

Two ways to get graphical summaries of numeric variables are the histogram and boxplots. Allow to visualize the distribution of the data and to identify possible outliers.

par(mfrow = c(1, 2))
# Histogram with additional density estimate
hist(cod$weight, freq = FALSE)
lines(density(cod$weight), col = 2, lwd = 2)
# Boxplot
boxplot(cod$weight, main = "Weight histogram")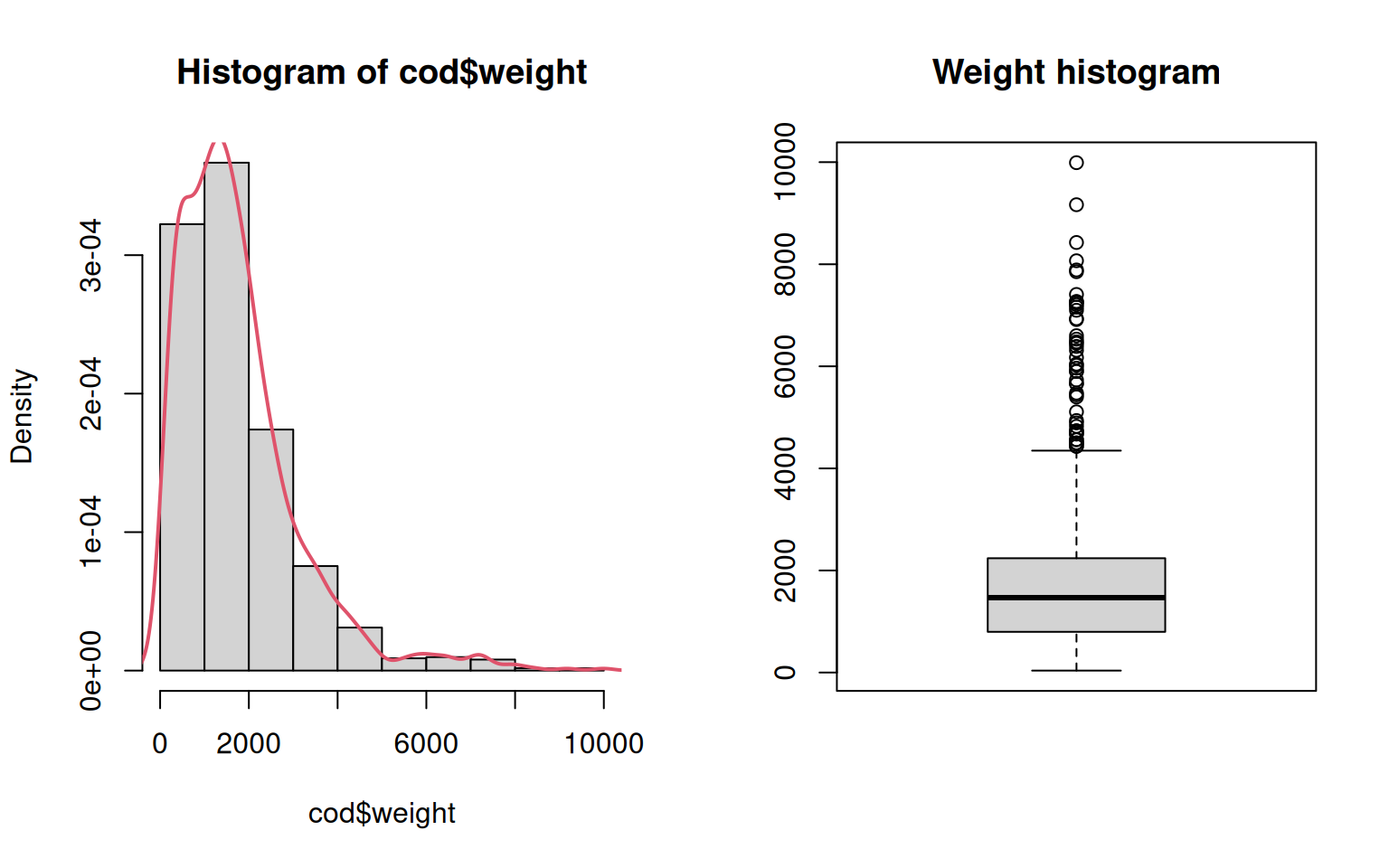

Details

  • Density of weight (i.e., area under curve equals \(1\)).
  • Default: Absolute frequencies, changed to density via freq = FALSE.
  • Further fine tuning possible via selection of breaks .
  • Added kernel density estimate (density()).
  • The Box-and-Whisker shows the same information in a different way (more aggregated).

14.2 Single categorical

When having categorical variables (factor) the summary statistics/plots used for numeric values are no longer meaningful. Whenever possible, the generic functions of R take care of this. In addition, we might use additional functions such as table(), xtabs(), and/or proportions().

Numerical summary

Let us have a look at:

  • Frequency tables.
  • Absolute vs. relative frequencies.
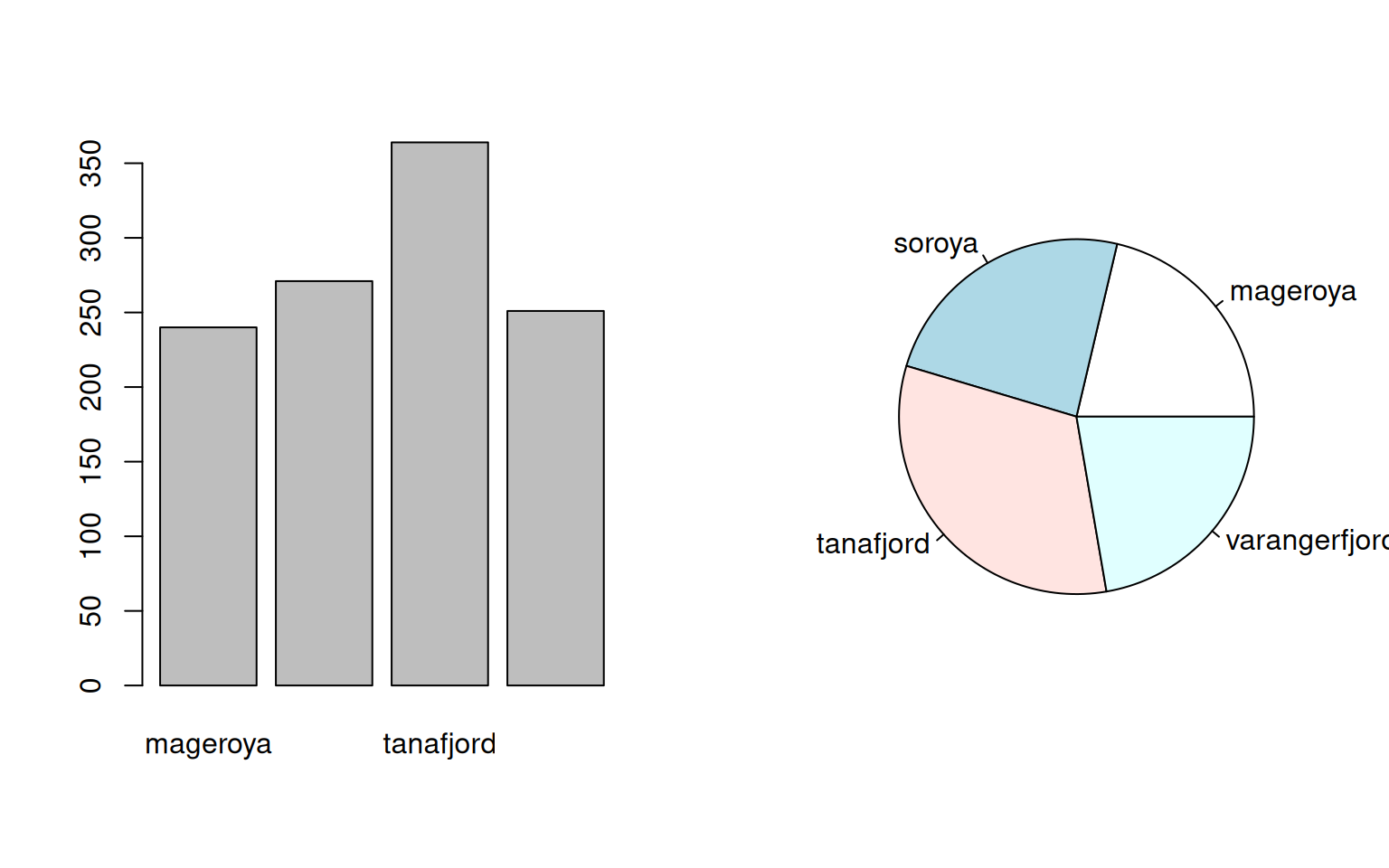
  • summary() vs. more flexible table() or formula-based xtabs().
summary(cod$area)
##      mageroya        soroya     tanafjord varangerfjord 
##           240           271           364           251
table(cod$area)
## 
##      mageroya        soroya     tanafjord varangerfjord 
##           240           271           364           251
xtabs(~ area, data = cod)
## area
##      mageroya        soroya     tanafjord varangerfjord 
##           240           271           364           251

As shown, xtabs(~ area, data = cod) works the same way as table(cod$area) but allows for more flexibility using the formula interface. We are interested in the number of male and female fishes (sex) in each of the 4 areas in the data set:

xtabs(~ area + sex, data = cod)
##                sex
## area            male female
##   mageroya       117    123
##   soroya         144    127
##   tanafjord      176    188
##   varangerfjord  115    136

By default, table() and xtabs() give us absolute counts. If interested in relative frequencies, proportions() can be applied on the return (prop.table() for R versions before version 4).

proportions(table(cod$area))
## 
##      mageroya        soroya     tanafjord varangerfjord 
##     0.2131439     0.2406750     0.3232682     0.2229130

In case we have a table with more than only one dimension the proportions can be calculated over the entire object or along one of the dimensions.

# The sum over all values equals to 1.0
proportions(xtabs(~ area + sex, data = cod))
##                sex
## area                 male    female
##   mageroya      0.1039076 0.1092362
##   soroya        0.1278863 0.1127886
##   tanafjord     0.1563055 0.1669627
##   varangerfjord 0.1021314 0.1207815
# The sum over each row equals to 1.0
proportions(xtabs(~ area + sex, data = cod), 1)
##                sex
## area                 male    female
##   mageroya      0.4875000 0.5125000
##   soroya        0.5313653 0.4686347
##   tanafjord     0.4835165 0.5164835
##   varangerfjord 0.4581673 0.5418327
# The sum over each column equals to 1.0
proportions(xtabs(~ area + sex, data = cod), 2)
##                sex
## area                 male    female
##   mageroya      0.2119565 0.2142857
##   soroya        0.2608696 0.2212544
##   tanafjord     0.3188406 0.3275261
##   varangerfjord 0.2083333 0.2369338

By multiplying the table by 100 you’ll get the percentages (relative frequencies in percent).

Graphical summary

We will have a look at the following:

  • Display frequencies by barplot().
  • plot(cod$area) is equivalent to barplot(table(cod$area)).
  • If majorities are to be brought out, pie() charts can be useful.
  • Both expect tabulated frequencies as input.
par(mfrow = c(1, 2))
tab <- table(cod$area)
barplot(tab)
pie(tab)

14.3 Two numerical

What if we would like to analyze the relationship between two numeric values?

Numerical summary

Correlation coefficient(s) via cor(). Default is the standard Pearson correlation coefficient, alternatives include the nonparametric Spearman’s \(\rho\).

cor(log(cod$length), log(cod$weight))
## [1] 0.9915759
cor(log(cod$length), log(cod$weight), method = "spearman")
## [1] 0.9862109

We can see that length and weight have a high correlation as expected as bigger (longer) fishes are expected to be heavier than smaller ones. We can see the advantage of using a log() transformation on both variables in the next section when visualizing the relationship.

Graphical summary

We can also visualize this relationship using the generic X-Y plot.

  • plot(x, y) not using the formula interface.
  • plot(y ~ x, data = cod) using the formula interface.
  • Using log() transformation for the first two plots, while plotting non-transformed observations in the last sub-figure.
par(mfrow = c(1, 3))
# x: log-weight, y: log-length
plot(log(cod$weight), log(cod$length))
# Using the formula interface
plot(log(length) ~ log(weight), data = cod)
# Same but not log transformed
plot(length ~ weight, data = cod)

14.4 One numeric, one categorical

What if having one numeric variable (using weight) and one categorical variable (area).

Numerical summary

What we can do is to calculate ‘grouped numerical summaries’ using either tapply() or aggregate().

# Average log-weight per area 
tapply(log(cod$weight), cod$area, mean)
##      mageroya        soroya     tanafjord varangerfjord 
##      7.257991      7.189640      7.171342      6.962064
# Same using aggregate()
aggregate(log(weight) ~ area, data = cod, FUN = mean)
##            area log(weight)
## 1      mageroya    7.257991
## 2        soroya    7.189640
## 3     tanafjord    7.171342
## 4 varangerfjord    6.962064

Graphical summary

Plotting one numeric value (left hand side of the formula) given a categorical variable (right hand side).

par(mfrow = c(1, 2))
plot(log(weight) ~ area, data = cod)
plot(log(weight) ~ area, data = cod, varwidth = TRUE)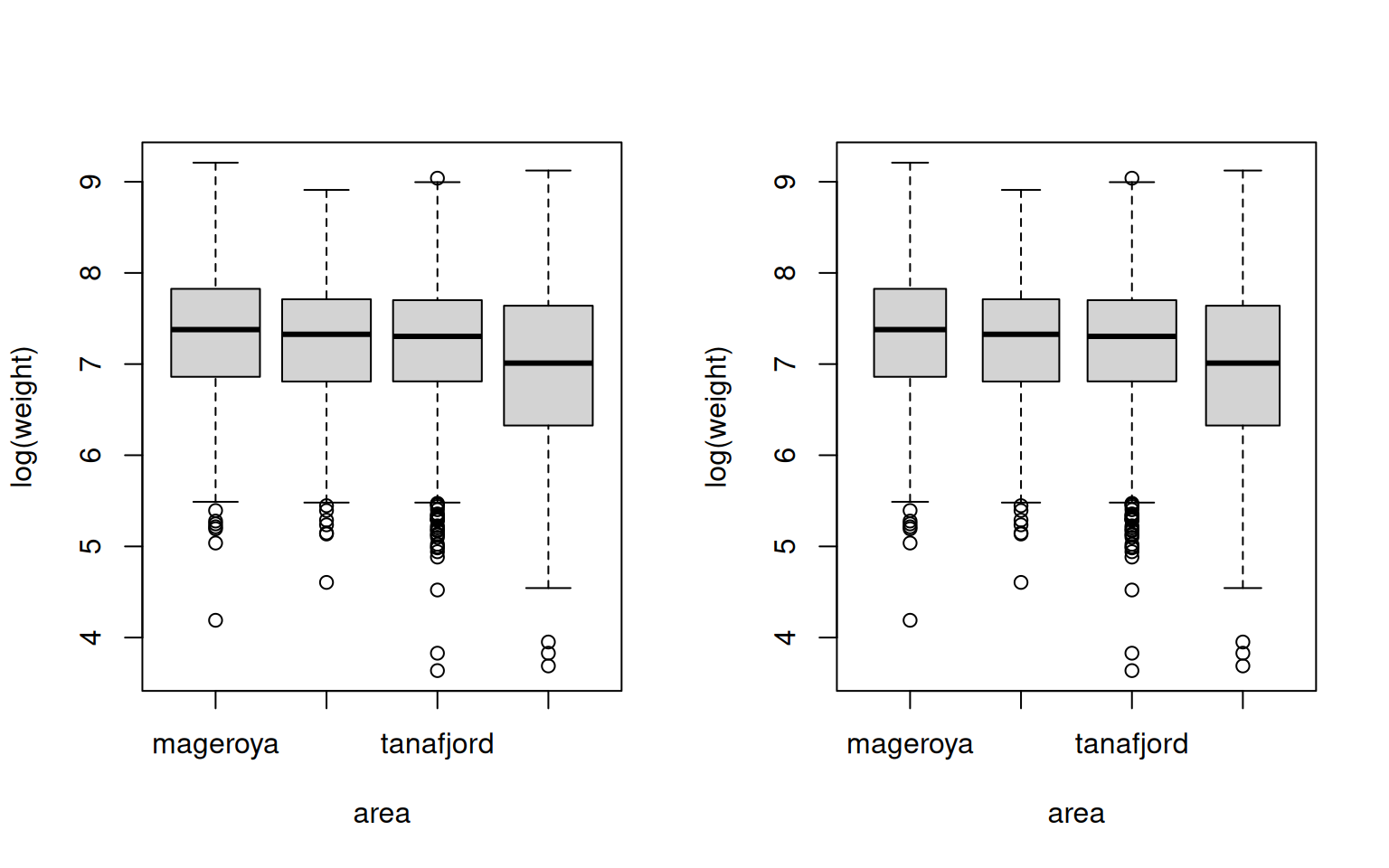

The boxplot

  • Coarse graphical summary of an empirical distribution.
  • Box indicates “hinges” (approximately the lower and upper quartiles) and the median.
  • “Whiskers” indicate the largest and smallest observations falling within a distance of \(1.5\) times the box size from the nearest hinge.
  • Observations outside this range are outliers (in an approximately normal sample).

Note that the two commands plot(y ~ x) and boxplot(y ~ x) both yield the same parallel boxplot if x is a factor.

14.5 Two categorical

Last but not least let us have a look at the analysis of two categorical variables. Let us use area (factor) and prevalence (logical). As the latter one is a logical variable and not a factor we sometimes need to turn it into a factor using factor(prevalence) below.

Numerical summary

  • Contingency table(s) via xtabs() (with formula interface) or table().
  • Conditional relative frequencies via proportions().
  • Logical as a factor with two levels (TRUE, FALSE) in table()/xtabs().
tab <- xtabs(~ prevalence + area, data = cod)
tab
##           area
## prevalence mageroya soroya tanafjord varangerfjord
##      FALSE      161    136       240            77
##      TRUE        79    135       124           174
proportions(tab, 2)
##           area
## prevalence  mageroya    soroya tanafjord varangerfjord
##      FALSE 0.6708333 0.5018450 0.6593407     0.3067729
##      TRUE  0.3291667 0.4981550 0.3406593     0.6932271

Graphical summary

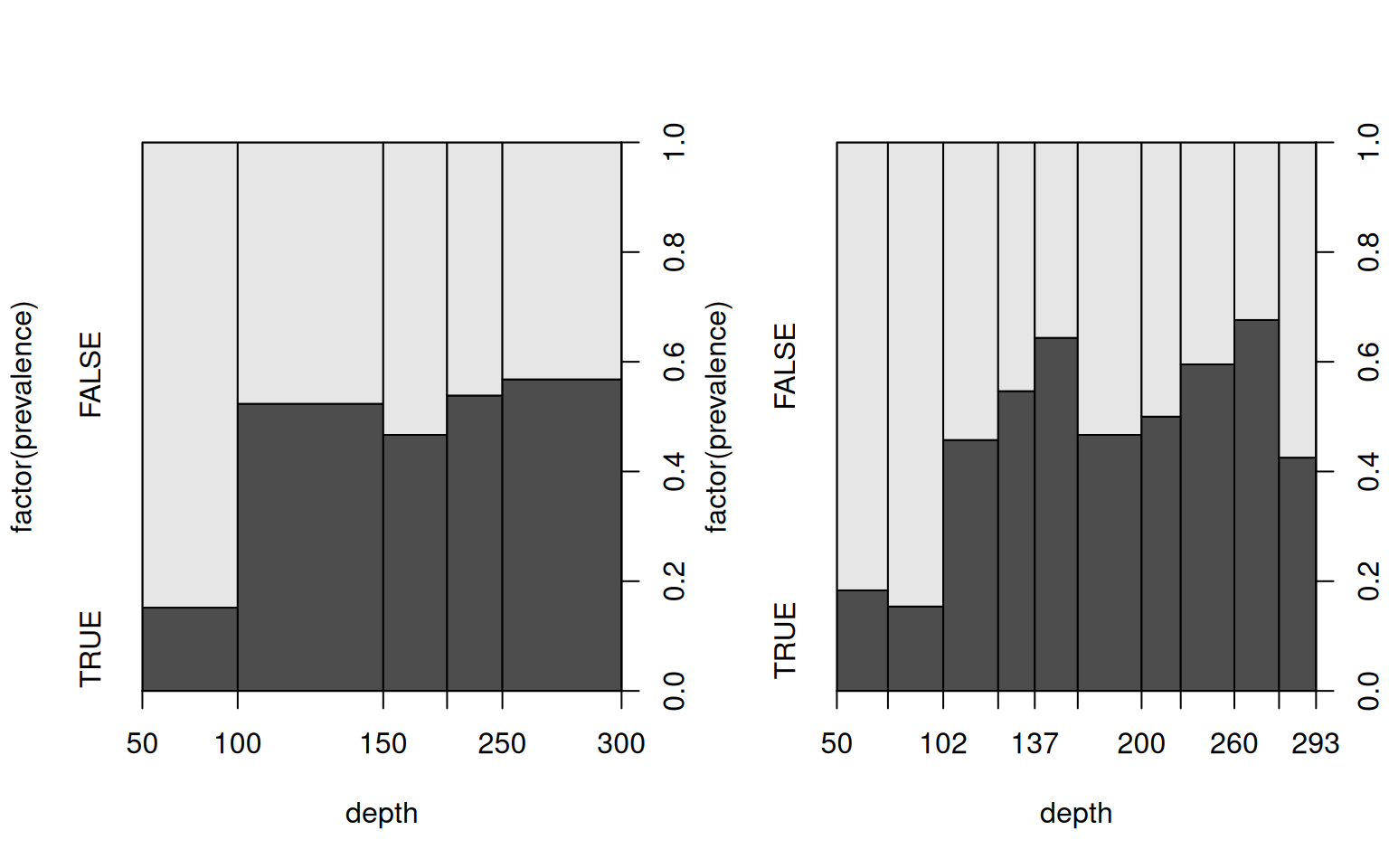
When having two categorical variables parallel boxplots will no longer work. Instead, R will create a so called mosaic plot.

A mosaic plot is a generalization of stacked barplots. The following variant is also called “spine plot”.

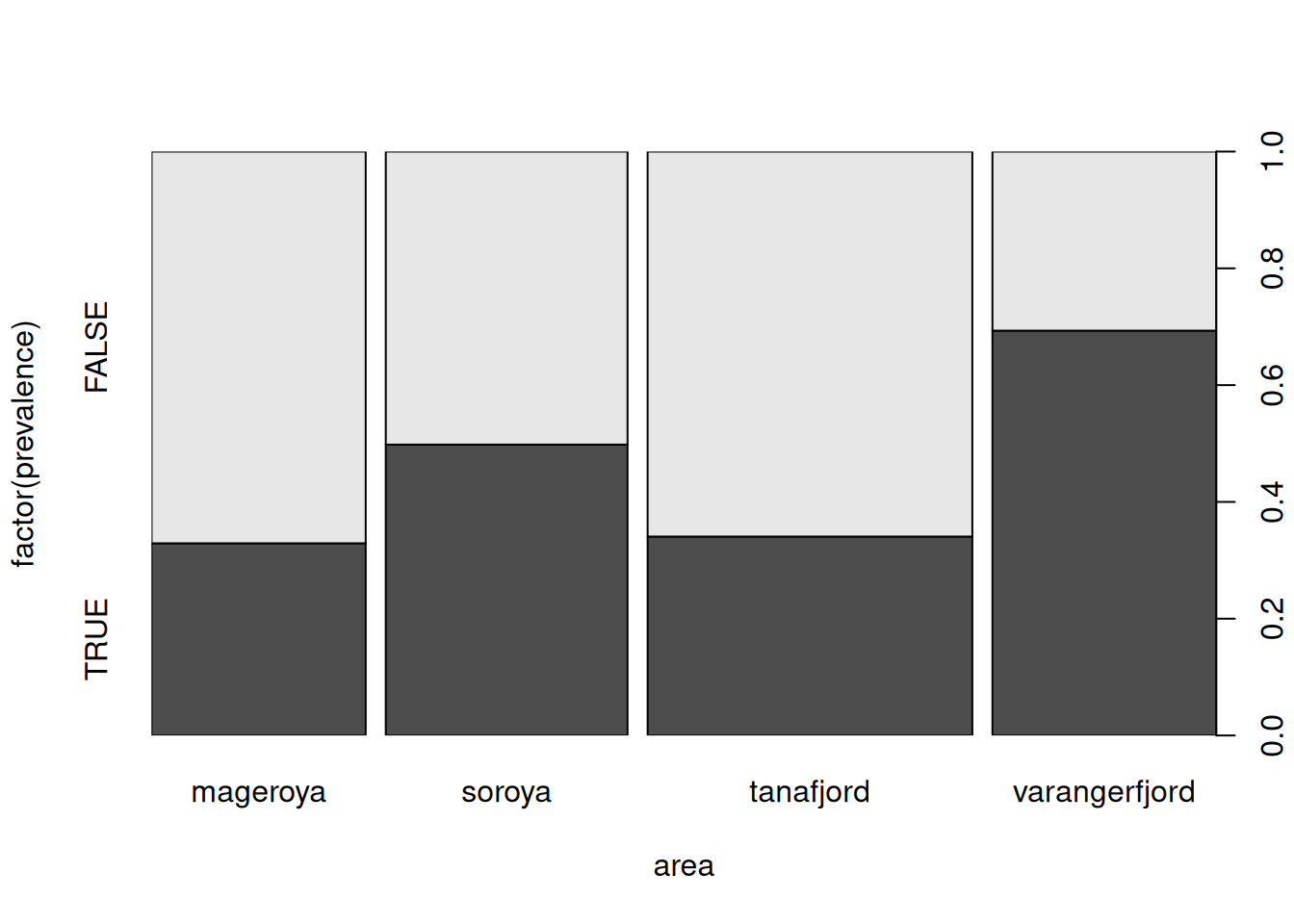
plot(factor(prevalence) ~ area, data = cod)

How to read: The heights of the bars correspond to the conditional distribution of factor(prevalence) given area. The bar widths visualize the marginal distribution of area.

If we plot a categorical variable against a numerical variable R will create a “Spinogram”. The Spinogram is a mosaic plot where R breaks he numerical variable into intervals (as in a histogram) and then employ the spine/mosaic plot as for two categorical variables.

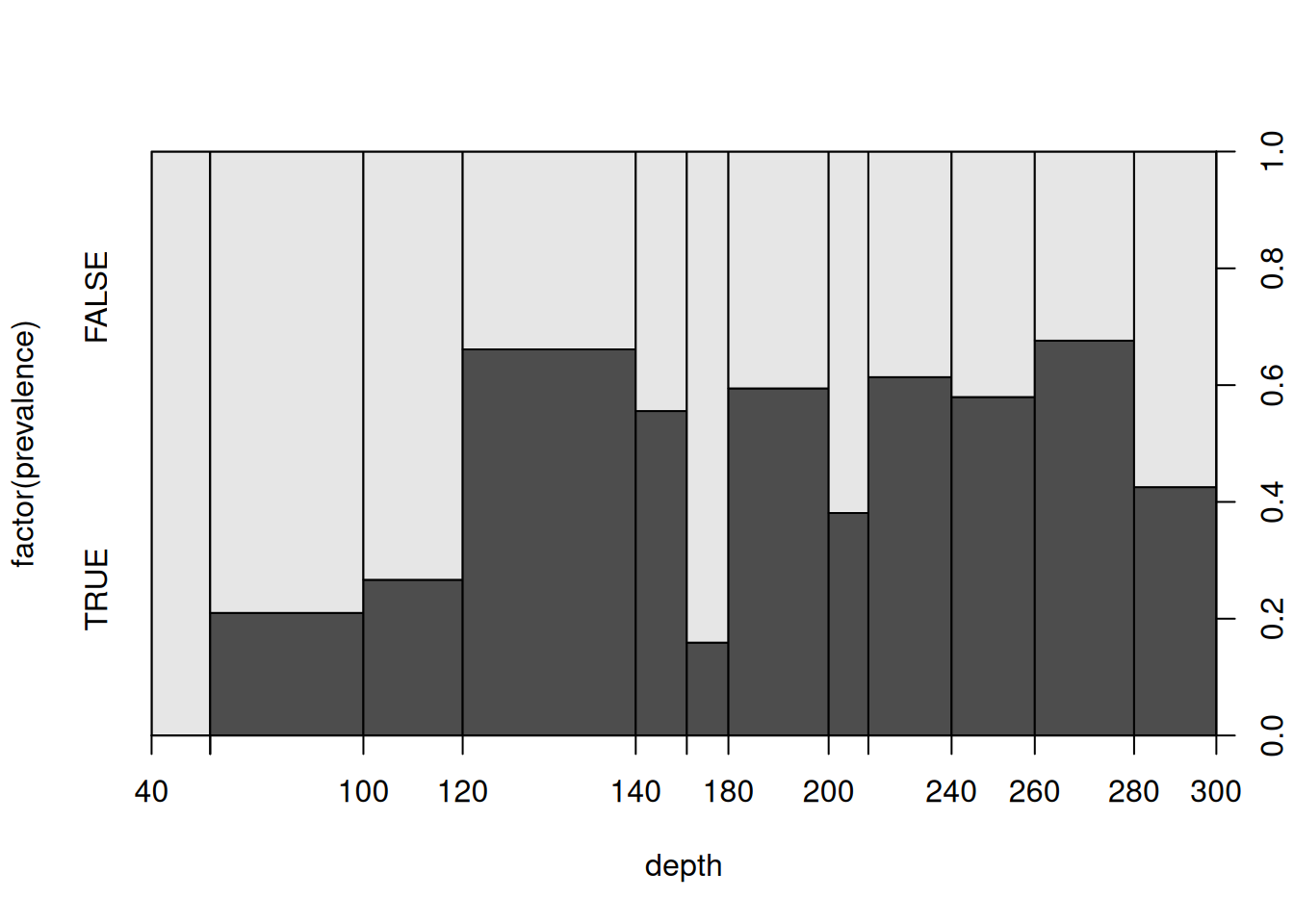
plot(factor(prevalence) ~ depth, data = cod)

As in a histogram the breaks are by default equidistant using some heuristic. Alternatively, the approximate number of (equidistant) breaks can be supplied or the desired breaks (based on deciles, here).

par(mfrow = c(1, 2))
plot(factor(prevalence) ~ depth, data = cod, breaks = 8)
plot(factor(prevalence) ~ depth, data = cod, breaks = quantile(depth, 0:10/10))