Chapter 13 Data Management

Before we start, let us quickly clarify what to expect in this chapter. Data management (how to deal with data sets) and data analysis (explore data, extract information from the data set, draw conclusions) cover a wide range of different topics and can get very complex. The goal of this chapter is to provide an important but relatively basic introduction to data management and some useful functions for exploratory data analysis using data frames in R.

Basic data management

  • Screening data sets, data sanity checks and data validation.
  • Prepare data for data analysis: Variable transformation, variable/data selection, data aggregation etc.

Basic exploratory data analysis

  • Next chapter!
  • Descriptive statistics.
  • Graphics.

For those who interested in learning more about these topics: the Digital Science Center and other departments of the Universität Innsbruck offer dedicated courses for “Data Management” and “Data Analysis” (as a particular instance, see Data Analytics on discdown.org).

13.1 General strategy

Before going into details, let us define a general strategy how to deal with data. This strategy is not specific to R and can be transferred to other programming languages or programs whenever dealing with (new) data sets.

Typical procedure/steps

  1. Importing data: Download and import data sets (see Chapter Reading & Writing).
  2. Data sanity checks:
    • Is the structure of the data set OK?
    • Initial class/type, dimension, …, for all variables.
    • Are there any missing or unrealistic values?
    • Use meta-information and data set description if available. Often contain useful information about the data, gaps, units, missing values, …
  3. Preparation:
    • Rename variables and levels.
    • Transform variables, factors/classes, unit conversions, combine information, …
    • Subset of variables and/or observations of interest.
  4. Exploratory analysis:
    • Descriptive statistics and visualizations.
    • Possibly aggregated within subgroups.
  5. If necessary: Iterate the steps above and adjust your code for preparing the data set.

Now – not earlier – we can start with the formal analysis of the data set, test our hypothesis, set up and estimate our regression models or whatever needed.

Why is this procedure so important?

  • Never trust a data set and use it “as it is” without thinking about it and check data at hand.
  • The quality of the data set is essential. If you don’t understand the data set, or the data set is simply incorrect/corrupted, your results may be complete rubbish. Or even worse: wrong, but not obviously wrong.
  • Helps to avoid wasting time. Nothing is more frustrating than spending days on developing scripts and functions just to find out that “the data set does not provide enough information to answer my (research) question” or “my results are useless as the data set is corrupt/incomplete/wrong”.

13.2 Useful functions

The table below shows a series of functions for the different steps when dealing with ‘data management’ and ‘data analysis’. As you should be familiar to most of them from the previous chapters, we will concentrate on the ones listed under preparation in the following table. The rest of the table can be seen as a recap of useful functions dealing with data and exploratory data analysis.

Task Function Description
Structure checks class() class of object/variable
typeof() type of object/variable
str() structure of an object
dim() dimension of rectangular objects
head() first \(n\) entries
tail() last \(n\) entries
names() names/variable names
names(x)[3] <- foo replace a specific (variable) name
levels(), nlevels() checking factor levels
...
Data checks summary() numerical summary
plot() generic X-Y plot (and other plot types)
is.na() check for missing values
duplicated() return duplicated elements/rows
anyDuplicated() returns \(\ne 0\) if duplicates are found, \(0\) else
unique() get unique elements/rows
min() get lowest value
max() get highest value
range() vector with minimum and maximum
...
Preparation transform() transform a data frame (add, remove, modify variables)
aggregate() aggregating data
reshape() reshape data frames (long form/wide form)
x[order(...), ] sort/order the observations of x
subset() subsetting observations and/or variables
...

Also

  • Try to plan the data management part of your project/task.
  • Adhere to good practices: Keep your code with comments etc., such that you can always reproduce the steps taken and check/fix/extend your code.
  • When processing different data sets (files) with same format: consider to write a function which imports and prepares the data set.

Disclaimer

  • In this chapter we will focus on ‘data management with data.frame objects’ only.
  • For generic functions – such as transform(), subset(), aggregate() – we will mainly discuss the respective data.frame methods.
  • The goal is an intelligible workflow with base R, e.g., efficiency is not discussed and additional packages are avoided (see next item).
  • A series of popular frameworks exist which go beyond base R. For some of your future tasks they might be required as they offer additional functionality or are more efficient (memory usage, efficiency). Examples of commonly used packages are data.table and dplyr.

Additional packages such as data.table or dplyr might get important once you have very large data sets where they easily outperform the base R functions. This, however, adds additional dependencies (additional packages are required to run your code/program).

Especially when using dplyr (part of Tidyverse) this introduces new objects. dplyr functions no longer return objects of class data.frame but ‘data frame alike objects’.

While mostly similar to base R data frames not all commands work the very same and you might need to adjust/rewrite your functions and scripts. Once you switch to dplyr it makes sense to use the entire Tidyverse framework which requires to read/learn how it works. For those interested, feel free to have a look at the websites for dplyr and tidyverse (general information/overview).

Note: Depending on a specific task one has to evaluate whether or not it is beneficial to stick to base R or use additional packages (efficiency, dependencies, knowledge, compatibility, …). For this online learning resource we decided to stick to base R (besides few cases).

13.3 Formula interface

Something which is relatively specific to R is the so called formula interface. Formulae are used in a wide range of (generic) functions when dealing with data sets and become very important when doing data analysis (e.g., data clustering, estimating regression models, …).

A formula allows to express a statistical model – or the relationship between different variables – in a compact symbolic form. A simple example of a formula is y ~ x (~ is called a tilde).

  • How to read: “y given x” or “y explained by x”.
  • Variable of interest: The left hand side of ~ is our target (y).
  • Explanatory variable: The right hand side of ~ are our explanatory variables or grouping variables (here only x).

For demonstration let us use a formula in combination with plot() given a simulated data set containing three variables y (target), a (numeric), and b (factor).

# Generate data set
set.seed(6020)
demo <- data.frame(y = c(rnorm(50, 10, 5), rnorm(30, 12, 3)),
                   a = c(runif(50, 0, 1), runif(30, 0.5, 2)),
                   b = as.factor(rep(c("one", "two"), c(50, 30))))
head(demo, n = 3)
##           y         a   b
## 1  8.289177 0.5731291 one
## 2 12.264335 0.2952761 one
## 3 13.084562 0.1958731 one

We are interested how y and a relate using a graphical representation of the data. The same for y and b. In other words, we would like to visualize

  • y given a \(\rightarrow\) y ~ a
  • y given b \(\rightarrow\) y ~ b
par(mfrow = c(1, 2)) # Two plots side-by-side
plot(y ~ a, data = demo, main = "y explained by a", col = ifelse(b == "one", 1, 2))
plot(y ~ b, data = demo, main = "y explained by b", col = "gray80")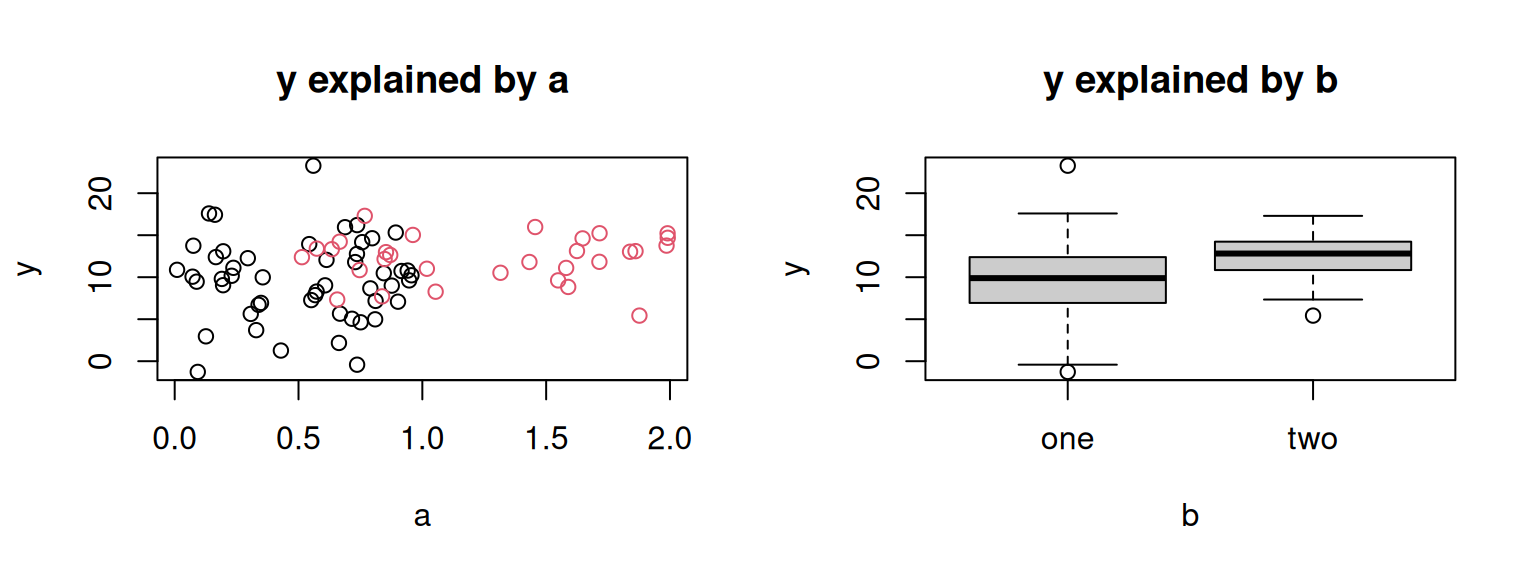

Besides some additional arguments for styling the plots, both commands are equal (plot(y ~ a), plot(y ~ b)) but yield two different types of plots. The target (left side of the formula) is plotted on the y-axis, the variable on the right hand side on the x-axis.

If both are numeric, the result is a scatter plot (left plot), if b is a character vector or factor, a box-and-whisker plot is getting created.

This is a simple example of how formulae are used, we will come back to it again later in this chapter. formula is an object class in R and can be handled like all other objects.

f <- y ~ a
c(class  = class(f),  typeof = typeof(f), length = length(f))
##      class     typeof     length 
##  "formula" "language"        "3"
plot(f, data = demo)   # Output suppressed in the book

13.4 Toy example

For the upcoming sections where some new functions are introduced, we will use a small toy data set containing six observations of soccer matches. Don’t worry, the data set is easy to understand even for non-soccer enthusiasts. The data set is used to analyze the performance of the team Manchester City (MCI) in the Premier League 2018/2019 against the three other teams that qualified for the Champions League.

(mci <- data.frame(
           team       = rep(c("Liverpool", "Chelsea", "Tottenham"), each = 2),
           type       = rep(c("home", "away"), 3),
           goals      = c(2, 0, 6, 0, 1, 1),
           against    = c(1, 0, 0, 2, 0, 0),
           possession = c(49.6, 49.4, 55.8, NA, 60.7, NA)
        ))
##        team type goals against possession
## 1 Liverpool home     2       1       49.6
## 2 Liverpool away     0       0       49.4
## 3   Chelsea home     6       0       55.8
## 4   Chelsea away     0       2         NA
## 5 Tottenham home     1       0       60.7
## 6 Tottenham away     1       0         NA

The teams always play two matches: One at their own city (Manchester, "home") and one in the home town of the opponent team ("away"). The data set contains:

  • team: The opponent team MCI is playing against.
  • type: Type of match: home match or away match.
  • goals: How many goals MCI scored (against the opponent team).
  • against: How many the opponent team scored against MCI.
  • possession: Percent of ball possession of MCI (Ballbesitz; unfortunately some data missing).

Dive into

Before learning the new functions in detail, let us dive into the analysis if the toy data set to get an impression where we are heading; no need to understand everything in detail in this section.

First, we are interested if there are missing values in the data set. We would see this in the summary output, but can also solve it programmatically by (i) counting the overall number of missing values or (ii) count the number of missing values per variable.

sum(is.na(mci))                           # (i) Total number of missing values
## [1] 2
sapply(mci, function(x) sum(is.na(x)))    # (ii) Number of missing values per variable
##       team       type      goals    against possession 
##          0          0          0          0          2

MCI plays against each team twice, one at home (in Manchester) and once in the city of the opponent. To make sure that we have no duplicated entries (wrong data) we check if there are any duplicated entries in team/type (the combination).

anyDuplicated(subset(mci, select = c(team, type)))
## [1] 0

0 indicates that no duplicated entries have been found and we can start working with this data set. Our toy data set contains goals and against but not yet the goal difference (who scored more/less) nor the points gained in the championship. The rules are:

  • \(3\) points: If they (MCI) beat the other team (victory).
  • \(1\) points: If both score the same (tie).
  • \(0\) points: If they (MCI) gets beaten (loss).

Let us add these two new variables using transform(); The first one (diff) contains the difference in goals scored by both teams, points contains the points gained in the Championship.

(mci <- transform(mci,
                  diff   = goals - against,
                  points = ifelse(goals < against, 0, ifelse(goals == against, 1, 3))))
##        team type goals against possession diff points
## 1 Liverpool home     2       1       49.6    1      3
## 2 Liverpool away     0       0       49.4    0      1
## 3   Chelsea home     6       0       55.8    6      3
## 4   Chelsea away     0       2         NA   -2      0
## 5 Tottenham home     1       0       60.7    1      3
## 6 Tottenham away     1       0         NA    1      3

We would like to analyze the performance of MCI in terms of points gained between home matches and away matches. Does the team perform better in their own city? Let’s see …

aggregate(points ~ type, data = mci, FUN = mean)
##   type   points
## 1 away 1.333333
## 2 home 3.000000

The function returns the average number of “points given type” and shows that MCI, on average, scored 3 points at home, while only 1.33 points when not playing in their own city.

What about the minimum/maximum of goals and against given the type of match and the number of points MCI got?

aggregate(cbind(goals, against) ~ type + points,
          data = mci, FUN = function(x) c(min = min(x), max = max(x)))
##   type points goals.min goals.max against.min against.max
## 1 away      0         0         0           2           2
## 2 away      1         0         0           0           0
## 3 away      3         1         1           0           0
## 4 home      3         1         6           0           1

Maybe we need the data set in a different form having points for the two types side by side instead of store in rows. We therefore subset the variables of interest and reshape the data set.

reshape(subset(mci, select = c(team, type, points)), sep = "_",
        direction = "wide", timevar = "type", idvar = "team")
##        team points_home points_away
## 1 Liverpool           3           1
## 3   Chelsea           3           0
## 5 Tottenham           3           3

This toy example shows that very detailed analyses can be done with only few lines of code. Let us have a look at the functions in more detail.

13.5 Finding duplicates

One step for checking the data set at hand is to check for duplicated entries. Base R comes with two functions called duplicated() and anyDuplicated().

  • duplicated(): Returns a logical vector of duplicated entries.
  • anyDuplicated(): Returns \(0\) if there are no duplicated entries, else the index (integer; always of length 1) of the very first duplicated entry.

The two functions serve specific purposes: duplicated() is used to identify the elements (observations in case of a data frame) containing duplicated entries, anyDuplicated() just tells us if there are any (at least one) duplicate and is very handy for conditional execution.

Usage Let us first check the usage of both functions.

## Default S3 method for duplicated
duplicated(x, incomparables = FALSE,
           fromLast = FALSE, nmax = NA, ...)

## Default S3 method for anyDuplicated:
anyDuplicated(x, incomparables = FALSE,
           fromLast = FALSE, ...)

Arguments

  • x: a vector or a data frame or an array or ‘NULL’.
  • incomparables: a vector of values that cannot be compared. FALSE is a special value, meaning that all values can be compared.
  • fromLast: logical indicating if duplication should be considered from the reverse side.
  • nmax: the maximum number of unique items expected (greater than one).

Example: We use the defaults for incompareables and nmax solely focussing on x and fromLast. By default (data frame) the entire observations are checked for duplicates. Thus, when asking for anyDuplicated(mci) we would expect a \(0\) as no observation is an exact copy of another one.

# Using the return (0 threaded as FALSE)
if (!anyDuplicated(mci)) cat("No duplicated observations found.\n")
## No duplicated observations found.

When checking for duplicated entries one has to define where duplicated are OK and where they are not allowed to occur. In this case: if the data set is correct, we should never have duplicated in “team/type”. On the other hand it is likely and OK that MCI scored the same number of goals against a specific team. Duplicates in “team/goals” are not a problem.

To search for duplicated entries in a subset of all variables, we make use of subset():

anyDuplicated(subset(mci, select = c(team, type)))  # Duplicates not OK
## [1] 0
anyDuplicated(subset(mci, select = c(team, goals))) # Duplicates OK
## [1] 6

In the second example anyDuplicated() reports that it found at least one duplicate in observation \(6\). Take care: there could be more than only one!

To demonstrate the difference between the two functions let us focus on the variable against (vector).

anyDuplicated(mci$against)
## [1] 3
duplicated(mci$against)
## [1] FALSE FALSE  TRUE FALSE  TRUE  TRUE
which(duplicated(mci$against))
## [1] 3 5 6

anyDuplicated() found the first duplicate on index \(3\). duplicated() returns richer information and tells us all elements which are duplicated (indices c(3L, 5L, 6L)). The duplicated entries in mci$against are the \(0\)s in the data set. As shown, the first occurrence (second row) is not considered to be a duplicate; only following elements showing the same value are marked as duplicated entries. We can change this behaviour using fromLast = TRUE, in this case the last occurrence is not considered to be a duplicated entry.

which(duplicated(mci$against, fromLast = TRUE))
## [1] 2 3 5

Keep in mind: The result of duplicated() (logical vector) can be used for subsetting and extracting specific observations, anyDuplicated() is used for control structures like sanity checks or value checks. We could use sum(duplicated(...)) > 0 to do the same check but this can be much slower on large data sets. anyDuplicated() stops as soon as it finds the first duplicate, while duplicated() always checks all data.

Exercise 13.1 Exercise: We have learned how to use unique() and duplicated(). Seems that these are closely related. Can we use duplicated() to find unique values?

We will work with the following vector of (pseudo-) random letters from A-D.

set.seed(100)
(x <- sample(LETTERS[1:4], 20, replace = TRUE))
##  [1] "B" "C" "B" "D" "C" "A" "B" "B" "D" "C" "D" "B" "B" "D" "C" "B" "B" "C" "C"
## [20] "C"
  • Try to make use of duplicated() to find all unique values.
  • Sort your unique vector from above and check if it is identical sort(unique(x)).

Solution. Unique: Straight forward, we directly sort the resulting vector lexicographically for later on. This, obviously, should result in a vector c(“A”, “B”, “C”, “D”).

(res_unique <- sort(unique(x)))
## [1] "A" "B" "C" "D"

Duplicated: We know that duplicated() returns a logical vector with elements set to TRUE if this element is a duplicate of an element which already occurred at least once.

This means that duplicated() always returns FALSE if an element first occurs (or is unique to that point). Thus, we can select all elements from x where duplicated() == FALSE or !duplicated().

sum(!duplicated(x)) # Must be four of them: A, B, C, D
## [1] 4
(res_duplicated <- x[!duplicated(x)])
## [1] "B" "C" "D" "A"

Perfect, we only have to sort and check if this is identical to the solution shown above:

identical(res_unique, sort(res_duplicated))
## [1] TRUE

Is sort() needed? Not in the example/solution shown above. But what happens if we specify fromLast = TRUE?

x[!duplicated(x, fromLast = FALSE)]
## [1] "B" "C" "D" "A"
x[!duplicated(x, fromLast = TRUE)]
## [1] "A" "D" "B" "C"

As you can see, this can change the order of the values. But: unique() has the same argument. Thus:

identical(unique(x, fromLast = TRUE), x[!duplicated(x, fromLast = TRUE)])
## [1] TRUE
identical(unique(x, fromLast = FALSE), x[!duplicated(x, fromLast = FALSE)])
## [1] TRUE

Note that x[!duplicated(x)] does the same as unique() and is about as fast, but we should use unique() when looking for unique values and duplicated() if we are interested in duplicates.

13.6 Transforming data

We have already learned how to replace, remove and add variables/elements in the two previous chapters Lists and Data frames. The function transform() is a convenience function to do the same in a slightly different way.

Usage

transform(`_data`, ...)

The function returns a modified version of the original data set.

Arguments

  • _data: The object to be transformed (typically a data frame).
  • ...: A series of “tag = value” arguments.

Example: As shown above this allows us to add variables, but also to modify or delete existing ones. Let us add a new dummy variable which is nothing else than LETTERS[1:6] and manipulate points by multiplying them by \(100\).

(mci <- transform(mci, dummy = LETTERS[1:6], points = points * 100))
##        team type goals against possession diff points dummy
## 1 Liverpool home     2       1       49.6    1    300     A
## 2 Liverpool away     0       0       49.4    0    100     B
## 3   Chelsea home     6       0       55.8    6    300     C
## 4   Chelsea away     0       2         NA   -2      0     D
## 5 Tottenham home     1       0       60.7    1    300     E
## 6 Tottenham away     1       0         NA    1    300     F

transform() takes the object mci, evaluates all tag = value arguments (important: tag = value not tag <- value!), appends them to the original object and returns it. As for subset() we can directly use the variable names (here points) and do not have to specify mci$points. If R finds the variable (goals) in the object provided as input, this variable will be taken for calculation. Note: it is not possible to directly use newly created variables within one transform() call (dummy in this case).

Return value: The return is a modified version of the original input mci.

We can also remove existing variables by assigning a NULL to them. As we have ‘messed up’ the points column, we fix this in the same call.

(mci <- transform(mci,
                  dummy = NULL,              # Delete this variable
                  points = points / 100))    # Fixing 'points'
##        team type goals against possession diff points
## 1 Liverpool home     2       1       49.6    1      3
## 2 Liverpool away     0       0       49.4    0      1
## 3   Chelsea home     6       0       55.8    6      3
## 4   Chelsea away     0       2         NA   -2      0
## 5 Tottenham home     1       0       60.7    1      3
## 6 Tottenham away     1       0         NA    1      3

Job done. We could, of course, do the same without using the function transform(). Check out the following exercise.

Exercise 13.2 Practical exercise: Instead of using transform() we could do the same using the $ operator (or subsetting) and assign/modify/delete variables. Try to start over with the original object mci and do the same without using transform().

# Start with this object (called mci2 now)
(mci2 <- data.frame(
           team    = rep(c("Liverpool", "Chelsea", "Tottenham"), each = 2),
           type    = rep(c("home", "away"), 3),
           goals   = c(2, 0, 6, 0, 1, 1),
           against = c(1, 0, 0, 2, 0, 0)
        ))
##        team type goals against
## 1 Liverpool home     2       1
## 2 Liverpool away     0       0
## 3   Chelsea home     6       0
## 4   Chelsea away     0       2
## 5 Tottenham home     1       0
## 6 Tottenham away     1       0
  • Add new variable diff and points.
  • Add new variable dummy containing LETTERS[1:6], multiply points by a factor of 100.
  • Delete dummy, correct points.

Solution. Starting from this object:

# Start with this ..
(mci2 <- data.frame(
          team    = rep(c("Liverpool", "Chelsea", "Tottenham"), each = 2),
          type    = rep(c("home", "away"), 3),
          goals   = c(2, 0, 6, 0, 1, 1),
          against = c(1, 0, 0, 2, 0, 0)
       ))
##        team type goals against
## 1 Liverpool home     2       1
## 2 Liverpool away     0       0
## 3   Chelsea home     6       0
## 4   Chelsea away     0       2
## 5 Tottenham home     1       0
## 6 Tottenham away     1       0

Adding two new columns:

mci2$diff   <- mci2$goals - mci2$against
mci2$points <- ifelse(mci2$goals < 0, 0, ifelse(mci2$goals == mci2$against, 1, 3))
head(mci2, n = 2)
##        team type goals against diff points
## 1 Liverpool home     2       1    1      3
## 2 Liverpool away     0       0    0      1

Add dummy, multiply points:

mci2$dummy  <- LETTERS[1:6]
mci2$points <- mci2$points * 100
head(mci2, n = 2)
##        team type goals against diff points dummy
## 1 Liverpool home     2       1    1    300     A
## 2 Liverpool away     0       0    0    100     B

Remove dummy, correct points:

mci2$dummy  <- NULL
mci2$points <- mci2$points / 100

# Print final result
print(mci2)
##        team type goals against diff points
## 1 Liverpool home     2       1    1      3
## 2 Liverpool away     0       0    0      1
## 3   Chelsea home     6       0    6      3
## 4   Chelsea away     0       2   -2      3
## 5 Tottenham home     1       0    1      3
## 6 Tottenham away     1       0    1      3

We can also do it this way, but needs more typing than when using the transform() function and makes the commands harder to read, especially if you do more complex calculations to create new variables.

Besides transform() two additional functions exist which can become very handy but will not be discussed further in this chapter.

  • within(): Similar to transform(); no longer uses tag = value syntax but takes a series of expressions evaluated in an encapsulated environment (inside the function). Allows to directly use newly created variables if needed.
  • with(): Does not modify the original object; only returns one new variable. Sometimes handy to reduce code complexity.
  • For both: Check out documentation on ?with or ?within (same).

13.7 Aggregating data

A new useful generic function is aggregate() allowing for data aggregation. You may notice similarities to tapply(), one of the loop replacement functions, however, aggregate() is no loop replacement function itself.

aggregate() (as it is a generic function) can be applied to objects of different classes, we will cover use cases in this chapter: Using the generic S3 function for data.frames and the generic S3 function for formula (see Formula interface).

Usage: The manual page (see ?aggregate) shows how to use the function in these two cases (data.frame’s/formula):

## S3 method for class 'data.frame'
aggregate(x, by, FUN, ..., simplify = TRUE, drop = TRUE)

## S3 method for class 'formula'
aggregate(x, data, FUN, ...,
          subset, na.action = na.omit)

In both cases (shown below) we can achieve the same results. However, the default behaviour of the two S3 methods distinctly differ, especially for processing multivariate data.

Usage: S3 method for class ‘formula’ (if the first input is a formula; see ?aggregate for details).

Arguments for use with data.frame’s:

  • x: an R object (vector or data.frame).
  • by: a list of grouping elements, each as long as the variables in the data frame x. The elements are coerced to factors before use.
  • FUN: a function to compute the summary statistics which can be applied to all data subsets.

Arguments for use with formula:

  • formula: a formula, such as y ~ x or cbind(y1, y2) ~ x1 + x2, where the y variables are numeric data to be split into groups according to the grouping x variables (usually factors).
  • data: a data frame (or list) from which the variables in formula should be taken.
  • FUN: a function to compute the summary statistics which can be applied to all data subsets.
  • ...: further arguments passed to or used by methods.
  • subset: an optional vector specifying a subset of observations to be used (as in subset()).
  • na.action: a function which indicates what should happen when the data contain NA values. The default is to ignore missing values in the given variables (Note: will be discussed in detail later).

Example: We are interested in the mean number of points given type of match (points ~ type; as shown above) and calculate the mean() based on our data set mci.

aggregate(points ~ type, data = mci, FUN = mean)
##   type   points
## 1 away 1.333333
## 2 home 3.000000

Instead of the arithmetic mean we can also return the range (minimum to maximum) of the goal differences given type of match or the 0.5 quantile (\(50\%\) percentile; also known as median) of points given type of match. Note that probs is forwarded to our function quantile() via the ... argument of aggregate().

# Range of goal differences
aggregate(diff ~ type,   data = mci, FUN = range)
# .5 quantile: same as FUN = median.
aggregate(points ~ type, data = mci, FUN = quantile, probs = 0.5)

If we would like to aggregate multiple variables at once, the left hand side (target) of the formula can be extended using cbind() using a comma separated list of variable names to be aggregated.

aggregate(cbind(goals, against, diff, points) ~ type, data = mci, FUN = mean)
##   type     goals   against       diff   points
## 1 away 0.3333333 0.6666667 -0.3333333 1.333333
## 2 home 3.0000000 0.3333333  2.6666667 3.000000

In this case the arithmetic mean is calculated for all four variables on the left hand side at once, calculating the mean for goals ~ type, against ~ type, diff ~ type and points ~ type. We can also extend the right hand side of the formula, e.g., aggregating the number of goals given type and points.

aggregate(goals ~ type + points, data = mci, FUN = range)
##   type points goals.1 goals.2
## 1 away      0       0       0
## 2 away      1       0       0
## 3 away      3       1       1
## 4 home      3       1       6

The combination of type and points are now unique (all possible combinations), the latter two columns contain minimum/maximum number of goals. When only looking at the last line of the result we get the information that:

  • Whenever MCI played a home match and got \(3\) points (won the match) they scored at least \(1\) up to \(6\) goals.

Exercise 13.3 tapply() versus aggregate(): Just for practicing, use tapply() instead of aggregate() to get the same information. We have seen the following command above, aggregating the points difference given type (home/away).

# Mean point difference given type of match (home or away)
(res_agg <- aggregate(diff ~ type, data = mci, FUN = mean))
##   type       diff
## 1 away -0.3333333
## 2 home  2.6666667
  • Use tapply() to get the same information (mean difference).
  • Advanced: try to create an object identical to res_agg using the result returned by tapply().

Solution. Disclaimer: This exercise is just for practicing purposes, in reality you would stick to aggregate() which is much more convenient.

tapply(): We are interested in mci$diff and group by mci$type; that is what the formula diff ~ type expresses used when calling aggregate(), and apply the function mean().

# Store result on res_tapply
(res_tapply <- tapply(mci$diff, mci$type, FUN = mean))
##       away       home 
## -0.3333333  2.6666667

Make the objects identical: tapply() returns us a named vector while aggregate() returns a data frame. Furthermore, the variable names are gone when using tapply().

What we need to do:

  • Create a new data frame.
  • Take the names of the named vector res_tapply and store this information as the first variable type.
  • Take the content (mean) and store it as second variable diff.
  • Compare the two objects.
res <- data.frame(type = names(res_tapply), diff = as.numeric(res_tapply))
identical(res_agg, res)
## [1] TRUE

Not good practice as we have hard-coded variable names when creating the new data frame (data.frame(type = ..., diff = ...)). But as mentioned, this was just for practicing.

Not using formula interface: It is possible to use aggregate() not using the formula interface. In case our first input to aggregate() is not a formula but e.g., a data frame the usage of the function differs.

Usage: Using a data frame as first input (similar to what we have seen for tapply().

## S3 method for class 'data.frame'
aggregate(x, by, FUN, ..., simplify = TRUE, drop = TRUE)
  • x: an R object (data frame in this case).
  • by: a list of grouping elements, each as long as the variables in the data frame ‘x’. The elements are coerced to factors before use.
  • FUN: Out function to be applied.

Example: Let us do the same as above.

aggregate(mci[, c("goals", "against", "diff", "points")],
          by = list(mci$type), FUN = mean)
##   Group.1     goals   against       diff   points
## 1    away 0.3333333 0.6666667 -0.3333333 1.333333
## 2    home 3.0000000 0.3333333  2.6666667 3.000000

Getting the same information and an object similar to using the formula interface.

Aggregation with missing values

When evaluating functions such as sum() or mean() on data with missing values, R’s default strategy is to return NA for the result. Alternatively, one often removes or omits the missing values prior to evaluating the function (typically by setting na.rm = TRUE).

In principle, the same can be done when aggregating data with missing values. However, the question how to remove missing values becomes more complex when multivariate data is aggregated.

  1. Conceptually, there are two strategies: The NAs for all variables can be handled simultaneously, i.e., the entire row of data is omitted when there is at least one NA (complete cases). Or, alternatively, the NAs can be dealt with per variable (available cases).
  2. In aggregate(), the defaults for dealing with missing values differ between the default method (available cases) and the fomula method (complete cases).
  3. Both methods can carry out both strategies, though.

As shown above, the variable possession contains 2 missing values. Let us assume to be interested in the average number of goals as well as the average possession for each type of game (home vs. away) by performing the aggregation once (i) using the S3 method for data frames (default) and once (ii) using the formula interface.

# (i) Aggregation using the default interface
aggregate(subset(mci, select = c(goals, possession)), list(mci$type), FUN = mean)
##   Group.1     goals possession
## 1    away 0.3333333         NA
## 2    home 3.0000000   55.36667
# (ii) Using the formula interface
aggregate(cbind(goals, possession) ~ type, data = mci, FUN = mean)
##   type goals possession
## 1 away     0   49.40000
## 2 home     3   55.36667

Both work (no errors, no warnings) but show different results due to the different default behaviour of the two methods.

  • Default: uses all available cases for aggregation, thus also using the rows containing missing values.
  • Formula: only uses the complete cases, thus removing all observations (rows) which contain at least one missing value before aggregating the data.

The figure below illustrates the difference between the two cases.

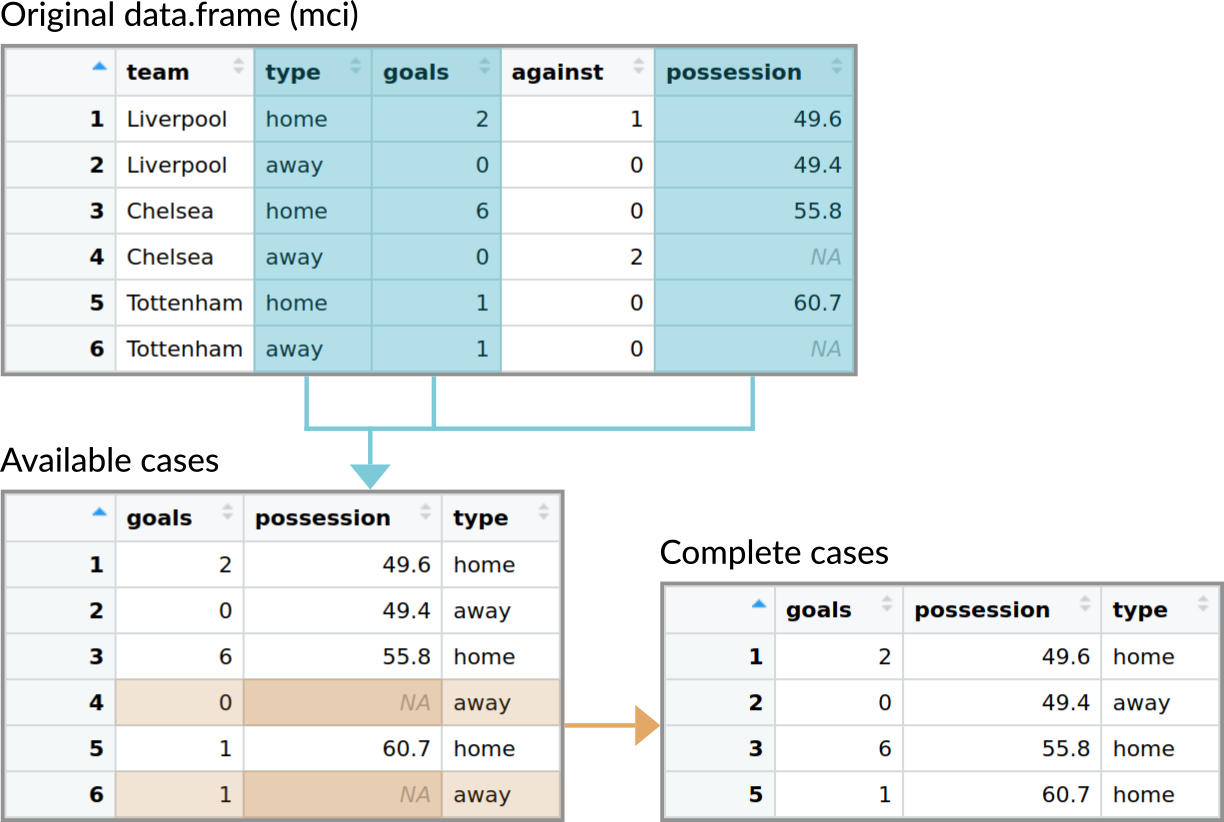
Illustration of the data used when aggregating data with either the default method for data.frames (uses available cases by default) and when using the method with a formula (uses complete cases by default).

Figure 13.1: Illustration of the data used when aggregating data with either the default method for data.frames (uses available cases by default) and when using the method with a formula (uses complete cases by default).

As shown at the beginning of this section (usage; see also ?aggregate) this is due to the default argument of the methods. The default method for data frames has no special argument on how to deal with missing values, the formula method uses na.action = na.omit.

In both cases we can change the behavior if needed. In case of the default method we can specify the additional argument na.rm = TRUE. As this is none of the argument of the function itself, it will be forwarded to our FUN. Thus, instead of using mean(...) it will call mean(..., na.rm = TRUE).

aggregate(subset(mci, select = c(goals, possession)), list(mci$type), FUN = mean,
          na.rm = TRUE) # <- additional argument
##   Group.1     goals possession
## 1    away 0.3333333   49.40000
## 2    home 3.0000000   55.36667

Note that we no longer have NAs in the aggregated result, however, the average number of goals differs from the result above as it uses the goals of all matches (the mean goals are based on 3 values each, for possession it uses 3 values for type = "home" but only one for type = "away").

When using the formula interface we can specify na.action = na.pass which lets missing values pass by, in other words using all available cases. This results in the very same result as when using the default method (without na.rm = TRUE).

aggregate(cbind(goals, possession) ~ type, data = mci, FUN = mean, na.action = na.pass)
##   type     goals possession
## 1 away 0.3333333         NA
## 2 home 3.0000000   55.36667

Thus, be aware of possible missing values when using aggregate to be sure to get the result you want.

13.8 Reshaping data

Re-shaping data from what is called a ‘long format’ to a ‘wide format’ is frequently needed. Base R comes with the function reshape() which allows to convert a data set from one form into another. Our toy data set is currently in the long format – let us first have a look at this data set in long and wide format focussing on team, type and points only.

##        team type points
## 1 Liverpool home      3
## 2 Liverpool away      1
## 3   Chelsea home      3
## 4   Chelsea away      0
## 5 Tottenham home      3
## 6 Tottenham away      3
##        team points.home points.away
## 1 Liverpool           3           1
## 3   Chelsea           3           0
## 5 Tottenham           3           3

This function is not changing data, but putting it in different shape (re-shape). Let us define the team as our ‘entity’. In the long format the ‘entity’ (team) can occur multiple times, while in the wide format each ‘entity’ only occurs once while all information is stored in the variables.

Important: In statistics and economics a common format for handling data are “panel data” where we typically have observations for a series of entities (e.g., persons, countries) over time (e.g., happiness over years, gross domestic product over years). This specific type of information is the motivation behind the function reshape() provided by base R and the names of its arguments which can make the use of reshape() somewhat confusing.

We can think about our object mci the same way: we have some entities (team) and varying information (points). Instead of time (years) the information varies with the type of match. type is the attribute which links the entity team to the varying information.

Note: Won’t be used extensively in this book/our course, but keep in mind this exists as it might become very handy when working with data sets in the future which often come in the ‘long format’, while we might need the ‘wide’ format to analyze the data.

Example: Our mci data set is currently in a long format. To get to the wide format (as sown above) we can call the following command:

(mci_wide <- reshape(mci,
                     direction = "wide",     # Reshape to 'wide'
                     v.names   = "points",   # Varying variables/variables of interest
                     idvar     = "team",     # Grouping (in rows)
                     timevar   = "type",     # Grouping (in columns)
                     drop      = c("possession", "diff", "goals", "against"))) # Drop them
##        team points.home points.away
## 1 Liverpool           3           1
## 3   Chelsea           3           0
## 5 Tottenham           3           3

The data set is re-shaped to the wide format. idvar defines the variable containing the entity (team) and timevar the attribute which connects the entity to the data in v.names. This also works from wide to long, however, rather complicated.

Instead: Let us have a look at two functions from an additional package called tidyr which might be easier to understand. The package provides two functions called:

  • pivot_longer(): converts wide to long.
  • pivot_wider(): converts long to wide.

Let us use the object mci once again and convert it to wide and back. Again, only team, type, goals and diff will be used for simplicity.

library("tidyr")  # Might need to be installed once

(mci_wide <- pivot_wider(subset(mci, select = c(team, type, points)),
                         names_from = "type", values_from = "points"))
## # A tibble: 3 × 3
##   team       home  away
##   <chr>     <dbl> <dbl>
## 1 Liverpool     3     1
## 2 Chelsea       3     0
## 3 Tottenham     3     3

What we get as a result is a ‘tibble data frame’ as tidyr is part of Tidyverse which could be converted to a pure data frame using as.data.frame() if needed. Let us now take the mci_wide and re-shape back to a long format.

(mci_long <- pivot_longer(mci_wide, cols = c(home, away),
                          names_to = "type", values_to = "points"))
## # A tibble: 6 × 3
##   team      type  points
##   <chr>     <chr>  <dbl>
## 1 Liverpool home       3
## 2 Liverpool away       1
## 3 Chelsea   home       3
## 4 Chelsea   away       0
## 5 Tottenham home       3
## 6 Tottenham away       3

What we can see is that we do not have the same object as before. This data set only contains three variables, namely team (entity), type (attribute) and points (value) which is known as the entity-attribute-value model.

Once more: Keep this in mind but don’t worry, will not be used intensively for the rest of this book.

13.9 Subsetting data

We have already learned how the function subset() works in Subchapter ‘Subsetting data frames’. For the sake of completeness:

Usage

subset(x, subset, select, drop = FALSE, ...)

Arguments

  • x: object to be subsetted.
  • subset: logical expression indicating elements or rows to keep; subsetting observations/rows.
  • select: expression, indicating columns to select from a data frame; subsetting variables/columns.
  • drop: passed on to ‘[’ indexing operator; allows to drop data frame attributes if only one variable is returned (to get a vector).

Examples

subset(mci, subset = goals > 3, select = c(team, type, goals))
##      team type goals
## 3 Chelsea home     6
subset(mci, against == 0, select = goals, drop = TRUE)
## [1] 0 6 1 1

13.10 Sorting & Ordering

One step of preparing our data set is to sort (change the order) of the observations. There is no dedicated function to sort() a data frame. Instead we make use of order() in combination with subsetting by index.

Usage

order(..., na.last = TRUE, decreasing = FALSE,
      method = c("auto", "shell", "radix"))

Important arguments

  • ...: a sequence of numeric, complex, character or logical vectors, all of the same length.
  • decreasing: logical. Should the sort order be increasing or decreasing?
  • na.last: for controlling the treatment of ’NA’s.

Examples

Order/sort by one variable against, decreasing (lexicographically).

# Order by 'against', decreasing
mci[order(mci$against, decreasing = TRUE), ]
##        team type goals against possession diff points
## 4   Chelsea away     0       2         NA   -2      0
## 1 Liverpool home     2       1       49.6    1      3
## 2 Liverpool away     0       0       49.4    0      1
## 3   Chelsea home     6       0       55.8    6      3
## 5 Tottenham home     1       0       60.7    1      3
## 6 Tottenham away     1       0         NA    1      3

Order/sort by two variables type and goals; increasing (default). First the data set is sorted by type. If a specific value in type occurs more than once, the second variable (goals) is used to sort the observations given this type.

# Order by 'type' first, 'goals' second, increasing
mci[order(mci$type, mci$goals), ]
##        team type goals against possession diff points
## 2 Liverpool away     0       0       49.4    0      1
## 4   Chelsea away     0       2         NA   -2      0
## 6 Tottenham away     1       0         NA    1      3
## 5 Tottenham home     1       0       60.7    1      3
## 1 Liverpool home     2       1       49.6    1      3
## 3   Chelsea home     6       0       55.8    6      3

13.11 Real world example

After introducing a general strategy how to import, check, transform, and aggregate data based on a very simple toy data set let us apply these steps on a larger real world data set. In this last section we will use an XLSX file “cod.xlsx” (click to download) from Zuur et al. (2009) originally taken by Hemmingsen et al. (2005; Marine Pollution Bulletin).

The data set was used to investigate the distribution of a specific blood parasite in Cods (Kabeljau). This parasite transmitted via Leeches (Blutegel) which like to lay their eggs on the carapace (Panzer/Schale) of the red king crab (rote Königskrabbe) which has been put into the Barents Sea in the 1960s by the Russians to serve as a resource of food.

Figure 1 and 2b from the original publication [Hemmingsen et al. 2005](https://doi.org/10.1016/j.marpolbul.2004.11.005).

Figure 13.2: Figure 1 and 2b from the original publication Hemmingsen et al. 2005.

The hypothesis

  • The more crabs, the more the Leech reproduce.
  • The more Leech, the more the parasite is transmitted to the Cods.

Data set information

  • XLSX (Excel) file format (cod.xlsx).
  • Contains 1254 observations; 1254 Cods fished.
    • intensity: Intensity of parasite infection.
    • prevalence: Boolean value; parasite present?
    • area/year/depth: Where and when the Cod was caught.
    • weight/length/sex/age: Information about the fish.
    • stage: Stage of the leech (life-cycle; the leech must leave the fish host at a later stage and lay its eggs).

(1) Importing the data set

First we need to import the data set using readxl in this case and investigate the returned object.

library("readxl")
cod <- data.frame(read_excel("cod.xlsx")) # Convert to data frame

read_excel() returns a ‘tibble data frame’ which we can easily convert to a base R data frame (not necessary).

head(cod, n = 3)
##   intensity prevalence     area year depth weight length sex stage age
## 1         0          0 mageroya 1999   220    148     26   0     0   0
## 2         0          0 mageroya 1999   220    144     26   0     0   0
## 3         0          0 mageroya 1999   220    146     27   0     0   0

(2) Data sanity checks

Once imported we can perform data sanity checks. Is the structure of the object OK? Do we have missing values? Are all values valid and meaningful?

str(cod)
## 'data.frame':    1254 obs. of  10 variables:
##  $ intensity : num  0 0 0 0 0 0 0 0 0 0 ...
##  $ prevalence: num  0 0 0 0 0 0 0 0 0 0 ...
##  $ area      : chr  "mageroya" "mageroya" "mageroya" "mageroya" ...
##  $ year      : num  1999 1999 1999 1999 1999 ...
##  $ depth     : num  220 220 220 220 220 220 220 194 194 194 ...
##  $ weight    : num  148 144 146 138 40 ...
##  $ length    : num  26 26 27 26 17 20 19 77 67 60 ...
##  $ sex       : num  0 0 0 0 0 0 0 0 0 0 ...
##  $ stage     : num  0 0 0 0 0 0 0 0 0 0 ...
##  $ age       : num  0 0 0 0 0 0 0 0 0 0 ...

What we get is a data frame with 1254 observations and 10 variables whereof 9 are numeric and 1 character. To check the range of the values (minimum/maximum) and the number of missing values we have a look at summary().

summary(cod)
##    intensity         prevalence         area                year     
##  Min.   :  0.000   Min.   :0.0000   Length:1254        Min.   :1999  
##  1st Qu.:  0.000   1st Qu.:0.0000   Class :character   1st Qu.:1999  
##  Median :  0.000   Median :0.0000   Mode  :character   Median :2000  
##  Mean   :  6.183   Mean   :0.4536                      Mean   :2000  
##  3rd Qu.:  4.000   3rd Qu.:1.0000                      3rd Qu.:2001  
##  Max.   :257.000   Max.   :1.0000                      Max.   :2001  
##  NA's   :57        NA's   :57                                        
##      depth           weight           length            sex       
##  Min.   : 50.0   Min.   :  34.0   Min.   : 17.00   Min.   :0.000  
##  1st Qu.:110.0   1st Qu.: 765.5   1st Qu.: 44.00   1st Qu.:1.000  
##  Median :180.0   Median :1432.0   Median : 54.00   Median :1.000  
##  Mean   :176.2   Mean   :1704.3   Mean   : 53.45   Mean   :1.411  
##  3rd Qu.:235.0   3rd Qu.:2222.5   3rd Qu.: 62.00   3rd Qu.:2.000  
##  Max.   :293.0   Max.   :9990.0   Max.   :101.00   Max.   :2.000  
##                  NA's   :6        NA's   :6                       
##      stage            age       
##  Min.   :0.000   Min.   : 0.00  
##  1st Qu.:1.000   1st Qu.: 3.00  
##  Median :1.000   Median : 4.00  
##  Mean   :1.409   Mean   : 4.07  
##  3rd Qu.:2.000   3rd Qu.: 5.00  
##  Max.   :4.000   Max.   :10.00  
##
  • We have some missing values in intensity, prevalence, weight, length.
  • weight: Maximum of 9990; is this realistic?
  • sex: Seems we have three values for sex (0 is wrong).
  • age: 84 fishes have age \(0\). Most likely as the age is rounded; thus OK.
  • prevalence: seems to be either TRUE (1) or FALSE (0).
  • Some variables (sex, area) are categorical data and should be transformed to factor.

Exercise 13.4 Start an R session yourself and try to look into these things in detail.

  • Programmatically get number of observations/variables, and class of all variables.
  • Programmatically extract the names of the variables which contain missing values.
  • Get the maximum of weight. Plot the vector weight. Is 9990 the only obviously wrong one?
  • Check unique values of sex. Count how often each of these values occurs in the data set.
  • Plot (hist()) the variable age. In addition, count how often age \(0\) occurs in the data set.

Solution. Number of observations/variables, class of all variables

The first one is simple:

n_obs  <- nrow(cod)
n_vars <- ncol(cod)
cat("We have", n_obs, "observations and", n_vars, "variables.\n")
## We have 1254 observations and 10 variables.

To get the class of each of the variables we could make use of sapply().

cod_classes <- sapply(cod, class)
table(cod_classes)
## cod_classes
## character   numeric 
##         1         9

Extract the names of the variables containing NA

We can count missing values in a vector using sum(is.na(x)). To apply this function to each variable individually, we again make use of sapply().

n_missing <- sapply(cod, function(x) sum(is.na(x)))
n_missing
##  intensity prevalence       area       year      depth     weight     length 
##         57         57          0          0          0          6          6 
##        sex      stage        age 
##          0          0          0

Using a relational operator to find the elements where we have at least one missing value (we could also use != 0 instead of > 0) and use this logical vector to get the names we need.

names(n_missing)[n_missing > 0]
## [1] "intensity"  "prevalence" "weight"     "length"

Get the maximum of weight

To get the maximum we have to take care that we have missing values in this variable.

max_weight <- max(cod$weight, na.rm = TRUE)
cat("Maximum weight is", max_weight, ".\n")
## Maximum weight is 9990 .

Let us plot the weight to see if this value is meaningful or an outlier.

hist(cod$weight)

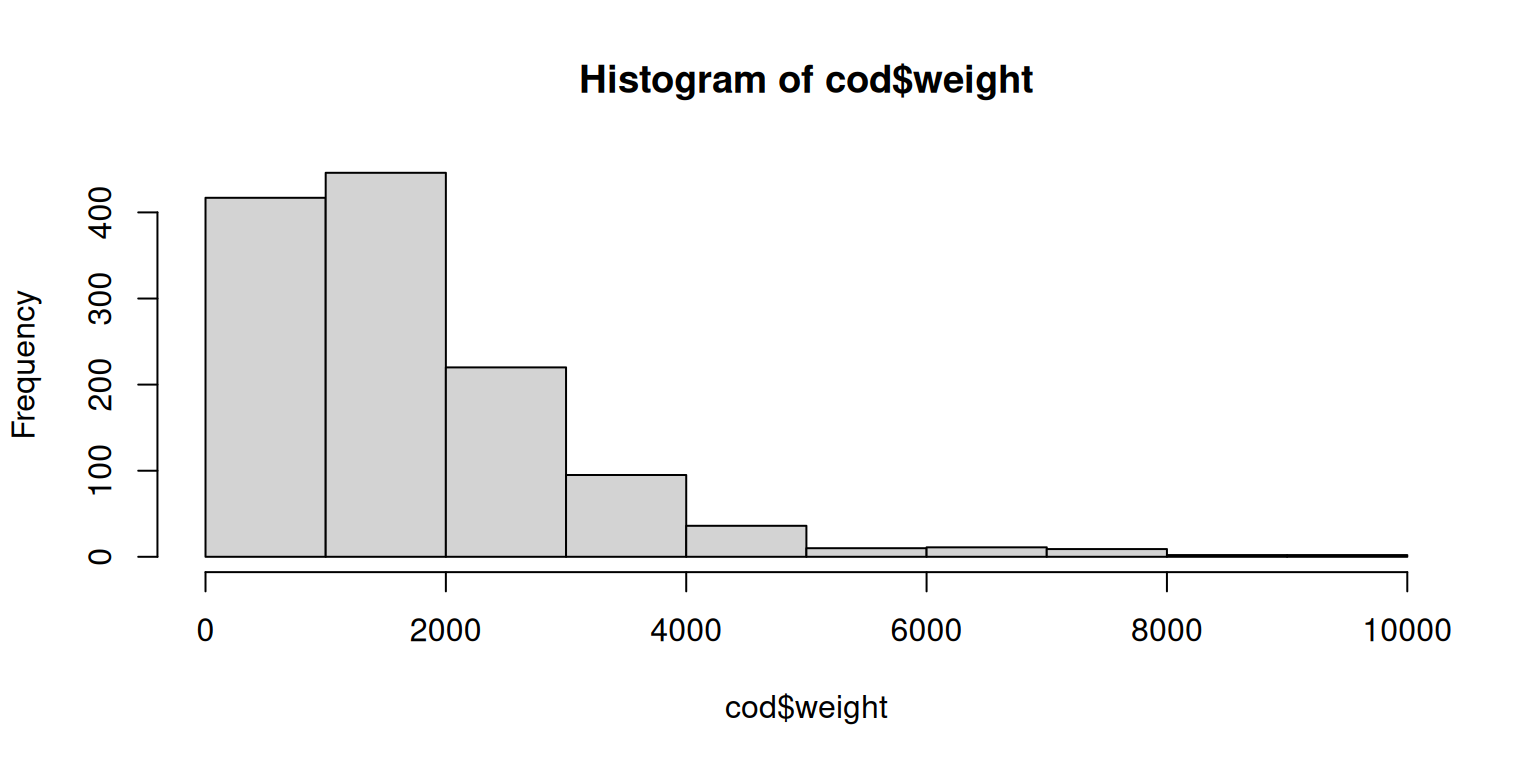
While most fishes weight below \(2000\), 9990 does not seem to be an outlier, but a decently heavy fish. Given this plot the values do look meaningful.

Check unique values of sex

Using unique() to find all unique values, or directly use table() which gives us both, all unique values and absolute counts (how often each one occurs).

table(cod$sex)
## 
##   0   1   2 
##  82 574 598

Plot (hist()) the variable age

Count number of fished being of age \(0\) and plot the distribution of age. We use the number of fishes being \(0\) in the title.

n_zero <- sum(cod$age == 0, na.rm = TRUE)
hist(cod$age, main = paste("Age of fish,", n_zero, "of age 0"))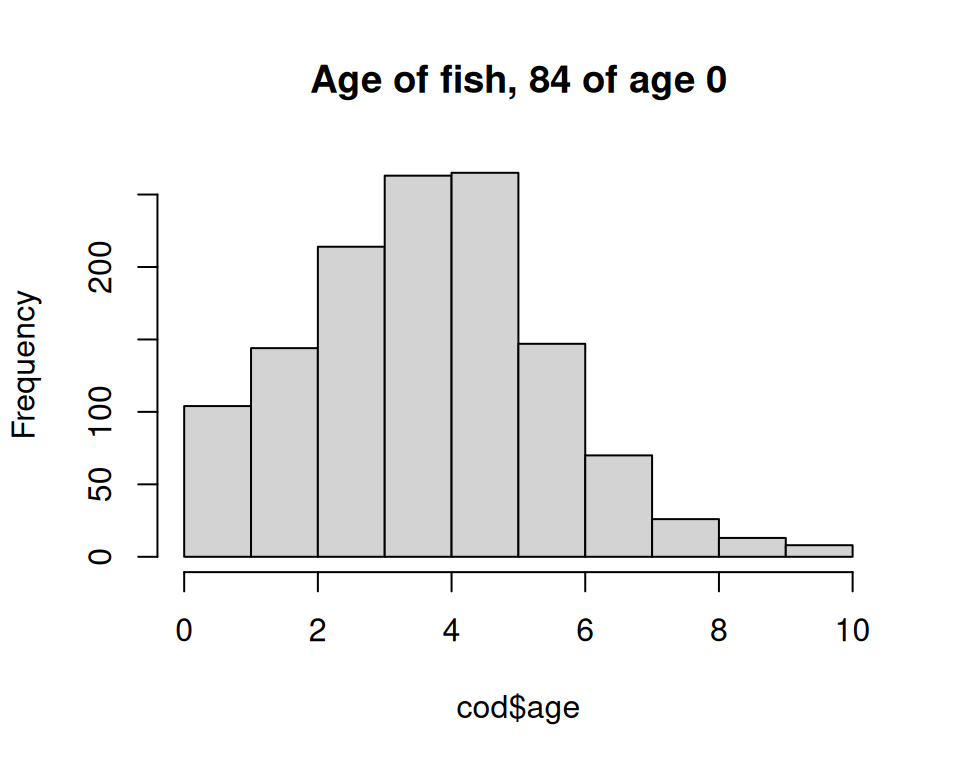

(3) Preparation

Once we have identified problems we can now prepare our data set.

  • Rename variables: Not required in this case (except you prefer to do so).
  • Transform variables: We would like to transform some into factor/logical.
  • Subset: Subset the data set to remove data we don’t need (e.g., missing values, or sex == 0).

Transforming variables

We can use transform() to transform the three variables prevalence, area and sex all in one go.

cod <- transform(cod,
               prevalence = as.logical(prevalence),
               area       = as.factor(area),
               sex        = factor(sex, 1:2, c("male", "female")))
str(cod)
## 'data.frame':    1254 obs. of  10 variables:
##  $ intensity : num  0 0 0 0 0 0 0 0 0 0 ...
##  $ prevalence: logi  FALSE FALSE FALSE FALSE FALSE FALSE ...
##  $ area      : Factor w/ 4 levels "mageroya","soroya",..: 1 1 1 1 1 1 1 3 3 3 ...
##  $ year      : num  1999 1999 1999 1999 1999 ...
##  $ depth     : num  220 220 220 220 220 220 220 194 194 194 ...
##  $ weight    : num  148 144 146 138 40 ...
##  $ length    : num  26 26 27 26 17 20 19 77 67 60 ...
##  $ sex       : Factor w/ 2 levels "male","female": NA NA NA NA NA NA NA NA NA NA ...
##  $ stage     : num  0 0 0 0 0 0 0 0 0 0 ...
##  $ age       : num  0 0 0 0 0 0 0 0 0 0 ...

Subsetting the data

We know there is fish with no sex. Due to our transformation they have been set to NA (we have not defined a level/label for 0). In addition we have fishes with no length and weight, and observations where the intensity is missing.

Let us remove all observations where on of these criteria occurs to remove all observations where we have missing values.

x <- subset(cod, !is.na(sex) & !is.na(intensity) & !is.na(length) & !is.na(weight))
sum(is.na(x))
## [1] 0
dim(x)
## [1] 1126   10

Alternatively we can use a function called na.omit(). na.omit() applied to a data frame removes all observations (rows) where we have at least one missing value. Let’s try …

cod <- na.omit(cod)
sum(is.na(cod))
## [1] 0
dim(cod)
## [1] 1126   10

(4) Exploratory analysis

As we now have a basic understanding of our data set and prepared the data set we can start working on the analysis. This, however, is part of the next chapter :).