Chapter 7 Conditional Execution

The functions discussed in Chapter 6 all had a simple and rather rigid structure: Exactly the same computations were carried out in the same order, regardless of what the input arguments were. To allow the code to become more flexible and adapt to the input arguments, we need additional “control flow” constructs which can decide whether or not to execute certain computations. The corresponding “if/else” constructs are no functions but special “reserved” statements in the R language.

In addition to the conditional execution, covered in this chapter, “control flow” also encompasses so-called “loops”, covered in the next Chapter 8, that allow some computations to be carried out multiple times or as often as required.

To illustrate flow control graphically, we use a basic (and not so serious) flow chart on how to do homework. This shows two conditional executions in the first two steps (“Do you have homework?” and “Is there something else you’d rather do?”) and then a repetitive execution (a “while loop” for “Is the homework due in less than 12 hours”?).

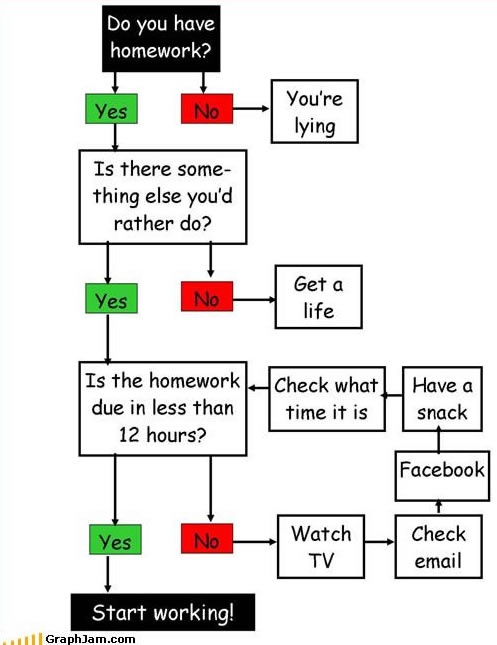
Figure 7.1: Source: GraphJam.com (offline).

There are three ‘different’ conditional statements we will go trough in this chapter.

If statements: Single expression with corresponding instruction.

If you are hungry: Eat something.
If the alarm clock rings: Get up.

If-else statements: Single expression with corresponding and alternative “else” instruction.

If the traffic light is green: Walk. Else: Stop.
If the coffee cup is empty: Refill. Else: Drink.

Multiple if statatements: Multiple expressions with corresponding instructions.

If warm and dry outside: Wear a T-shirt. Else if warm and rainy: T-shirt and a jacket. Else if cold and dry: Sweater. Else: Stay home.

As correctly declaring these statements critically depends on the logical conditional, let us first take a closer look at working with logical expressions in R before proceeding to using these in the construction of conditional statements.

7.1 Logical expressions

The basis of all these decisions are logical expressions using relational and logical operators (as well as value matching). We have already seen the different operators available in R in Chapter 4.5. If you need a refresh on this topic, please go trough the corresponding section again or check ?Comparison, ?logic, and ?match. Else proceed.

Logical expressions always return logical values: TRUE and/or FALSE. In case a certain logical expression (the condition) evaluates to TRUE, the corresponding code should be executed. Otherwise (else), i.e., when the condition evaluates to FALSE, that code should not be executed but possibly a different sequence of commands.

Just as a brief recap:

Relational operators: <, >, <=, >=, ==, !=.
Logical operators: !, &, |, &&, ||, xor().
Value matching: %in%, ! ... %in% (character operations).

Some examples:

Relational operators (x > y).
Logical operators (x & y).
Value matching ("Marc" %in% names).
all(), any(), all.equal().
Combinations of them (e.g., all(y < 0) | "Marc" %in% names).

Note: Logical expressions can also evaluate to NA (try NA > 3) which will result in an error when used for conditional execution. Thus, this may have to be considered when designing code.

Short and long form

As shown above, there are two forms (short vs. long) for the logical AND and OR operators &/| vs. &&|||.

Short form: & and | perform an elementwise comparison, possibly recycling one of the arguments to obtain two arguments of the same length. They return a logical vector of the same length as the objects compared.
Long form: && and || does not work for vectors but requires a single TRUE/FALSE for each condition. Evaluation proceeds only until the result is determined. For example, if the first argument in a && comparison is FALSE the second argument is not evaluated as it is already clear that the result will be FALSE.

Short-form operators

Some examples of logical expressions/comparison:

l1 <- c(TRUE, TRUE, FALSE, FALSE)
l2 <- c(TRUE, FALSE, TRUE, FALSE)
l1 & l2

## [1]  TRUE FALSE FALSE FALSE

The logical AND (&) is TRUE if the corresponding elements in both vectors are TRUE. Here, this is only the case for the first element as l1[1] and l2[1] are both TRUE while for the remaining elements at least one of the elements (or both) are FALSE.

The logical OR (|) works similarly but is TRUE if at at least l1 or l2 are TRUE (or both).

Last but not least we have the logical XOR (xor(), exclusive OR) which is TRUE if either l1 or l2 are TRUE but not both. For comparing the operators we set up the following matrix:

cbind(l1, l2, AND = l1 & l2, OR = l1 | l2, XOR = xor(l1, l2))

##         l1    l2   AND    OR   XOR
## [1,]  TRUE  TRUE  TRUE  TRUE FALSE
## [2,]  TRUE FALSE FALSE  TRUE  TRUE
## [3,] FALSE  TRUE FALSE  TRUE  TRUE
## [4,] FALSE FALSE FALSE FALSE FALSE

Long-form operators

In addition to these “vectorized” (short form) logical comparisons, we have the long-form operators && and ||. They only work with single TRUE and FALSE and, in contrast to the short form evaluate the their arguments (left to right) until the resulting logical value is determined. This can save computation time (is a bit faster) and can be very handy in some sitations (two examples included below).

For now, let us try to use the long-form logical and operator with the two logical vectors from above (l1, l2), both being of 4 (not 1).

l1 && l2

## Error in l1 && l2: 'length = 4' in coercion to 'logical(1)'

The same happens for l1 || l2, as only a single TRUEs or FALSEs are allowed. Let us write two new logical vectors of length 1 named m1 and m2 and try again:

m1 <- TRUE
m2 <- FALSE
m1 && m2    # Same as m1 & m2

## [1] FALSE

m1 || m2    # Same as m1 | m2

## [1] TRUE

In this example both && and & as well as || and | do the very the same. So what is the difference? In case of && and || R evaluates from left to right and exists as soon as the condition is met. To better understand the differences, two examples are shown below where the long form is useful.

First example: We have a single numeric x and would like to check if it is larger or than 0 or not. However, we know that it can also be NA. In this situation a simple if-else with x >= 0 will not work if x is NA.

x <- NA
if (x > 0) {
    cat("'x' is larger than zero\n")
} else {
    cat("'x' is not larger than zero\n")
}

## Error in if (x > 0) {: missing value where TRUE/FALSE needed

The problem is that x >= 0 results in an NA, but the condition requires a logical TRUE or FALSE. Here, we could make use of the long-form as follows:

if (!is.na(x) && x > 0) {
    cat("'x' is larger than zero\n")
} else {
    cat("'x' is not larger than zero - or a missing value (NA)\n")
}

## 'x' is not larger than zero - or a missing value (NA)

The long form evaluates from left to right, thus first checking if !is.na(x). In this case this evaluates to FALSE, thus there is no need to evaluate x > 0 as the full condition (logical &&) can never be TRUE.

Second example: Imagine we have an object data and we would like to check if (i) the object is a matrix and (ii) the matrix has exactly 3 columns. Thus, we need to check that the object is a matrix (is.matrix(data)) and that it has 3 columns (ncol(data) == 3).

# We actually have a matrix with 3 columns
data <- matrix(1:9, ncol = 3)
if (is.matrix(data) & nrow(data) == 3) {
    cat("Object 'data' is a matrix with 3 columns.\n")
}

## Object 'data' is a matrix with 3 columns.

What if data is not a matrix? In this case nrow(x) == 3 will not work as nrow(x) is NULL (vectors have no dimension) and comparing NULL == 3 will not result in a logical TRUE or FALSE therefore throwing an error.

# data is a vector
data <- 1:5
if (is.matrix(data) & nrow(data) == 3) {
    cat("Object 'data' is a matrix with 3 columns.\n")
}

## Error in if (is.matrix(data) & nrow(data) == 3) {: argument is of length zero

If we use && instead, R first checks if is.matrix(data) is TRUE. If not, there is no need to check the second condition, so it never executes nrow(data) == 3 therefore not running into the same error.

if (is.matrix(data) && nrow(data) == 3) {
    cat("Object 'data' is a matrix with 3 columns.\n")
}

Whilst not being used (needed) in this course, keep in mind that these long-form operators exists and can be very handy in certain situations.

Functions

In addition to these operators, a series of useful functions exist which can be used in conditional execution. We have already seen some of them in the previous chapters.

all(): Are all elements TRUE?
any(): Is at least one element TRUE?
all.equal(): Are two objects (nearly) equal?

The first two always return one single logical element (either TRUE or FALSE) or a single missing value (NA) and no longer a vector. Thus, they are used frequently in combination with conditional execution. The function all.equal() either returns TRUE or a character vector that describes the differences between the objects compared.

For illustration reconsider the vector l1 introduced above. As it contains both TRUE and FALSE values, all() is FALSE while any() is TRUE.

all(l1)

## [1] FALSE

any(l1)

## [1] TRUE

all.equal() is used for checking whether two objects, specifically two numeric vectors, are nearly equal. As we have already seen in Chapter 4 the == comparison may sometimes be too strict as small differences may occur between two numeric values due to the precision of arithmetic operations (e.g., recall that 1.9 - 0.9 == 1.0 evaluates to FALSE). Instead, all.equal() avoids this problem by allowing for a small tolerance.

The function also works on vectors. As a motivational example: We know that squaring the square root of x should yield x again. However, due to the precision of the involved arithmetic operations (square root, power of 2) the resulting vector y is just nearly equal but not identical.

x <- c(1, 2, 3, 4)
y <- sqrt(x)^2
y - x

## [1]  0.000000e+00  4.440892e-16 -4.440892e-16  0.000000e+00

The differences are basically zero; 4.44e-16 is \(4.44 \cdot 10^{-16}\), a very tiny difference which can be ignored in most (but not all) applications. Therefore, checking whether x and y are not identical and not all elements exactly equal but all elements are nearly equal when allowing for a small tolerance.

identical(y, x)

## [1] FALSE

all(y == x)

## [1] FALSE

all.equal(y, x)

## [1] TRUE

Note, however, that all.equal() only returns TRUE if two objects are nearly equal but not FALSE if they are not. Instead, a character description of the differences is returned in that case. Here, this is illustrated by comparing the given vector x with its square root which in this case is obviously not equal.

all.equal(sqrt(x), x)

## [1] "Mean relative difference: 0.7488414"

isTRUE() and isFALSE()

In conditional executation we rely on a single logical value, i.e., either TRUE or FALSE. However, given that some logical comparisons may also return NA and all.equal() may return a character vector, it is often handy to turn such values into TRUE or FALSE as well. This is the purpose of the functions isTRUE() and isFALSE() which - as their names convey - check whether their argument is a single TRUE or FALSE, respectively.

For example, isTRUE() is often used in combination with all.equal() to give TRUE if two objects are nearly equal and FALSE if not. With the vectors x and y from the example above:

isTRUE(all.equal(y, x))

## [1] TRUE

isTRUE(all.equal(sqrt(x), x))

## [1] FALSE

Another typical application of isTRUE() is to yield FALSE rather than NA in logical comparisons that include missing values. For illustration, consider the following vector x with two positive numbers and a missing values. If we wanted to assure that all elements of x are positive, we might use all(x > 0) but this is NA in this case.

x <- c(10, 20, NA)
x > 0

## [1] TRUE TRUE   NA

all(x > 0)

## [1] NA

By combining this with isTRUE() we can enforce a (non-missing) logical value. Here, this tells us that not all elements of x are positive.

isTRUE(all(x > 0))

## [1] FALSE

7.2 If statements

Based on the logical expression discussed above we can now declare the conditions that control the flow of scripts or functions. Let us start with the most basic version: a single if statement.

Basic usage: if (<condition>) { <action> }.

The <condition> has to be a single logical TRUE or FALSE.
If <condition> is evaluated to TRUE, the <action> is executed.

For example we want R to inform us via cat() that the variable x is smaller than 10 in case this is true.

x <- 8
if (x < 10) { cat("x is smaller than 10\n") }

## x is smaller than 10

The condition (here: x < 10) is always within round brackets if (...), the action is everything between the curly brackets ({ ... }). If the condition is evaluated to FALSE no action is executed, e.g., when x is 12.

x <- 12
if (x < 10) { cat("x is smaller than 10\n") }

Alternative syntax

Similar to the body of functions (see Chapter 6.9) the actions corresponding to if-statements can be written in separate lines or in a single line. Provided that the action consists of a single command only, it is also possible to omit the curly brackets, otherwise these are required. Hence all the following examples are equivalent.

Version 1: In separate lines.

if (x < 10) {
  cat("x is smaller than 10\n")
}

Version 2: In a single line.

if (x < 10) { cat("x is smaller than 10\n") }

Version 3: In a single line without brackets.

if (x < 10) cat("x is smaller than 10\n")

For more complex actions version 1 is the preferred one while for very simple actions version 3 is also frequently used.

7.3 If-else statements

The next extension of if-statements are if-else statements. In contrast to if-statements they have an additional else clause which is executed whenever the (if-)condition is evaluated to FALSE.

Basic usage:

Structure: if (<condition>) { <action 1> } else { <action 2> }.
If <condition> is evaluated to TRUE, <action 1> is executed. Else <action 2> is executed.

Let us take the same example as above where we check if a certain number is smaller than 10.

x <- 8
if (x < 10) {
    print("x is smaller than 10")
} else {
    print("x is larger or equal to 10")
}

## [1] "x is smaller than 10"

Alternative syntax

Again, if-else statements can be written in different ways. The three versions below are equivalent an all do the very same thing.

Version 1: The preferred one.

if (x < 10) {
    print("x is smaller than 10")
} else {
    print("x is larger or equal to 10")
}

## [1] "x is smaller than 10"

Version 2: One-liner.

if (x < 10) { print("x is smaller than 10") } else { print("x is larger or equal to 10") }

## [1] "x is smaller than 10"

Version 3: Without brackets.

if (x < 10) print("x is smaller than 10") else print("x is larger or equal to 10")

## [1] "x is smaller than 10"

These one-line forms are sometimes useful to make the code a bit more compact. However, they are harder to read, thus we recommend to use the first version (multiple lines, with curly brackets).

7.4 Nested conditions

If-else statements can also be nested. Nested means that one of the actions itself contains another if-else statement. Important: the two if-else statements are independent.

An example:

x <- 10
# 'Outer' if-else statement.
if (x < 10) {
    print("x is smaller than 10")
} else {
    # 'Inner' if-else statement.
    if (x > 10) {
        print("x is larger than 10")
    } else {
        print("x is exactly 10") 
    }
}

## [1] "x is exactly 10"

The procedure is the same as for a single if-else statement. The most outer is evaluated first. In case we end up in the else block of the ‘Outer’ if-else statement, we need to evaluate the second – ‘Inner’ – if-else condition.

Outer if-else statement: Is x < 10? FALSE: execute action in the else-block of the outer if-else statement.
Inner if-else statement: Is x > 10? FALSE: execute action in the else-block of the inner if-else statement, print "x is exactely 10").

7.5 Multiple if-else statements

Instead of nested (independent) if-conditions we can once again extend the concept by adding multiple if-else conditions in one statement. The difference to nested conditions is that this is one single large statement, not several smaller independent ones.

Basic usage:

Structure: if (<condition 1>) { <action 1> } else if (<condition 2>) { <action 2> } else { <action 3> }.
If <condition 1> evaluates to TRUE, <action 1> is executed.
Else <condition 2> is evaluated. If TRUE, <action 2> is executed.
Else, <action 3> is executed (if both, <condition 1> and <condition 2>, evaluate to FALSE).

Required parts:

Not limited to only 2 conditions.
Always needs one (and no more than one) if.
Can have 1 or more else ifs.
Can have no or 1 else-block (optional).

We can achieve the same result as above (Nested conditions) by writing the following statement.

x <- 10
if (x < 10) {
    print("x is smaller than 10")
} else if (x > 10) {
    print("x is larger than 10")
} else {
    print("x is exactly 10") 
}

This achieves the same result as the following statement which has no else-block.

x <- 10
if (x < 10) {
    print("x is smaller than 10")
} else if (x > 10) {
    print("x is larger than 10")
} else if (x == 10) {
    print("x is exactly 10") 
}

Else or no else: This strongly depends on the task. One advantage of else-block is that it captures all cases which are not considered by one of the conditions above. Thus, the else-block is something like the “fallback case”. In some other scenarios you only want to execute something if a strict condition is TRUE or do nothing. In such cases an else-block is not necessary.

Exercise 7.1 We have a variable x with one single numeric values and two different if-statements with the following conditions:

Version 1: if (x < 10), else if (x > 10), and else.
Version 2: if (x < 10), else if (x > 10), else if (x == 10) (no else).

Two questions to think about:

What if x is set to NA (x <- NA)? Will we end up in the else-block of statement ‘Version 1’ and get the "x is exactely 10" (which is wrong)?
Would it be better to use ‘Version 2’ without an else-block?

Solution. The answer is no to both questions.

One could think that the NA ends up in the else-block, but that is not true. As we have learned above, conditions must always evaluate to a logical TRUE or FALSE. NA < 10 results in an NA and R will throw an error when trying to evaluate the first condition (if (x < 10)). Thus, we will not unexpectedly end up in the else-block.

To answer the second question: There is no benefit of the second version. We check if x < 10 and x > 10. The only option left is x == 10, thus, in this case both are fail-save and do the very same.

In some situations it is not the case that there is only one option left, and you need to think if you want to have an else-block which captures everything else (or whatever your forgot), or if you want to add another explicit if-clause for specific cases.

Exercise 7.2 Below you can find a code chunk with a series of conditions. Try to read the code and think about what is going on without actually executing the code!

Possible answers

Does not work, an error occurs.
"x is larger than 10." will be printed.
"x is smaller or equal to 10." will be printed.
Nothing will be printed.

# (1) x is defined as 4
x <- 4

# (2) if-statement
if (x < 10) {
  x <- 100
}

# (3) if-else statement
if (x > 10) {
  print("x is larger than 10.")
} else {
  print("x is smaller or equal to 10.")
}

Solution. The correct answer is (3) "x is larger than 10." is printed.

Initializing x <- 4.
x < 10 is TRUE, wherefore x will be re-declared and set to x <- 100.
x is now 100 and thus x > 10 is TRUE: "x is larger than 10." is printed.

7.6 Return values

If-statements are not functions, but they still have a return value. By default, this return is not visible, but we can make use of it. The last time we are using the same example/statement, except that we do not print the character string, but return it and store the result (return value) on desc.

x <- 200
desc <- if (x < 10) {
    "x is smaller than 10"
} else if (x > 10) {
    "x is larger than 10"
} else if (x == 10) {
    "x is exactly 10"
}
# Print return value
print(desc)

## [1] "x is larger than 10"

To break it down: The second condition evaluates to TRUE. If we remove everything related to the if-else statement which is (i) unused or (ii) only used for the statement itself, we basically end up with this:

desc <- "x is larger than 10"

Note: This only works for checks where the condition evaluates to a single TRUE or FALSE. We can not use these if and if-else statements element-wise on a vector. To do so, we need to use the vectorized if.

7.7 Vectorized if

There is a special function which allows perform an if-else statement element by element for each element of a vector (or matrix).

Function: ifelse() for conditional element selection.

Arguments: ifelse(test, yes, no), where all arguments can be vectors of the same length (recycled if necessary). Works with matrices as well.
Return: Vector which contains yes elements if test is TRUE, else no elements.
Note: All elements of yes and no are always evaluated.

Practical example: we would like to find out if an numeric value is odd (ungerade) or even (gerade). This can be done using the modulo operator (see Vectors: Mathematical operations).

If the numeric value is divisible by 2 with rest 0, it is an even number, else odd. Two examples: 4 %% 2 returns 0 as \(2 \cdot 2 = 4\), rest \(0\), thus \(4\) must be an even number. 5 %% 2 returns 1 as \(2 \cdot 2 = 4\), rest \(1\), thus \(5\) must be odd.

(x <- 1:6)

## [1] 1 2 3 4 5 6

x %% 2 == 0      # Rest 0?

## [1] FALSE  TRUE FALSE  TRUE FALSE  TRUE

x %% 2 == 0 is our test-condition. We now want to return "even" if this is TRUE for a specific element in x, and "odd" if not. This can be done as follows:

#         test       yes      no
ifelse(x %% 2 == 0, "even", "odd")

## [1] "odd"  "even" "odd"  "even" "odd"  "even"

Another example: We will again test if a number is odd or even. If even, return x, else return -x. In this case the two arguments ‘no’/‘yes’ to ifelse() are vectors. Thus, all odd numbers should now be negative odd numbers, all even numbers should stay positive.

#          test     yes  no
ifelse(x %% 2 == 0,  x,  -x)

## [1] -1  2 -3  4 -5  6

Here all three arguments are vectors; x %% 2 == 0 is a logical vector of length 6, x and -x are two numeric vectors of the same length. If the test-condition evaluates to TRUE for a specific element the corresponding value from x is returned, else from -x.

Matrices: ifelse() also works with matrices. In case the input for the condition/test is a matrix, a matrix of the same size will be returned. The vectorized if works on the underlying vector, but adds the matrix attributes again at the end.

(x <- matrix(1:12, nrow = 3,
             dimnames = list(paste("Row", 1:3), paste("Col", LETTERS[1:4]))))

##       Col A Col B Col C Col D
## Row 1     1     4     7    10
## Row 2     2     5     8    11
## Row 3     3     6     9    12

ifelse(x %% 2 == 0, x, -x)

##       Col A Col B Col C Col D
## Row 1    -1     4    -7    10
## Row 2     2    -5     8   -11
## Row 3    -3     6    -9    12

Exercise 7.3 Exercise A: Start with a vector y <- 1:10. If the element in y is odd (ungerade), add + 1. If even (gerade), leave it as it is. The result should look as follows:

##  [1]  2  2  4  4  6  6  8  8 10 10

Exercise B: We will use some random numbers. For reproducibility we set a seed first:

set.seed(123)
y <- rnorm(10)

y now contains 10 numeric values. Use ifelse() to replace all negative values with "neg" and all others with "pos". If your seed is set correctly the result should be:

##  [1] "neg" "neg" "pos" "pos" "pos" "pos" "pos" "neg" "neg" "neg"

Exercise C Working with two matrices, requires a logical and or or for the condition (test).

(mat1 <- matrix(c(10, 0, -3, 15), nrow = 2))

##      [,1] [,2]
## [1,]   10   -3
## [2,]    0   15

(mat2 <- matrix(c(3, -1, -4, 17), nrow = 2))

##      [,1] [,2]
## [1,]    3   -4
## [2,]   -1   17

Use ifelse(), return NA when both, the element in mat1 and in mat2, are negative. Else return 0.

##      [,1] [,2]
## [1,]    0   NA
## [2,]    0    0

Solution. Solution for exercise A

If y %% 2 == 0 (even) return the elements from y as they are, if not (odd) use y + 1.

y <- 1:10
ifelse(y %% 2 == 0, y, y + 1)

##  [1]  2  2  4  4  6  6  8  8 10 10

We could of course also modify our test and ask for odd numbers (instead of even numbers). In this case we would also have to exchange the values for yes and no to get the correct result:

y <- 1:10
ifelse(y %% 2 != 0, y + 1, y)

##  [1]  2  2  4  4  6  6  8  8 10 10

Solution for exercise B

If y < 0 replace the element with "neg", else with "pos".

##  [1] "neg" "neg" "pos" "pos" "pos" "pos" "pos" "neg" "neg" "neg"

As "neg" and "pos" are character vectors of length 1, while y is of length 10, they will simply be recycled. Does the very same as the following line of code where we replicate "neg" and "pos" 10 times.

ifelse(y < 0, rep("neg", times = length(y)), rep("pos", times = length(y)))

##  [1] "neg" "neg" "pos" "pos" "pos" "pos" "pos" "neg" "neg" "neg"

Solution for exercise C

The condition is mat1 < 0 & mat2 < 0 which is TRUE when the elements in both values are below zero. If TRUE, return an NA, else 0.

mat1 <- matrix(c(10, 0, -3, 15), nrow = 2)
mat2 <- matrix(c(3, -1, -4, 17), nrow = 2)
ifelse(mat1 < 0 & mat2 < 0, NA, 0)

##      [,1] [,2]
## [1,]    0   NA
## [2,]    0    0

7.8 Sanity checks

A typical application for single if-statements are input checks of a function or before proceeding to the computations and are often used in combination with stop() or warning().

stop(): Will show an error warning and immediately stop execution.
warning(): Issues a warning, but the program will still be executed.

When used inside functions, this is called a sanity check. Sanity checks should be at the very beginning of the instructions of a function and check if the arguments are sane, or if the function should throw an error because the inputs are wrong.

Let us combine functions and if-statements to write a small example. We would like to have a function which calculates the square root of one single numeric value, a mathematical operation which is invalid for negative numbers.

Long form

Our function has one input argument x. Before we start the calculation, we check if the input argument x is valid. We will check for the three conditions below – if one is violated, we will stop execution and throw an error. Else we return the square root of argument x.

x must be numeric.
x must be of length 1.
x must be positive.

The function we are looking for looks as follows:

# Custom square root function
custom_sqrt <- function(x) {
    # Sanity check
    if (!is.numeric(x))   stop("Argument 'x' must be numeric!")
    if (!length(x) == 1L) stop("Argument 'x' must be of length 1!")
    if (x < 0)            stop("Argument 'x' must be positive (>= 0)!")

    # If not yet run into an error, do the calculation and return result
    res <- sqrt(x)
    return(res)
}

If we call the function with a valid argument, the function should return the desired result. Else one of the above error messages should show up – and the execution is immediately stopped.

# Working examples
custom_sqrt(9.0)

## [1] 3

custom_sqrt(25L)                  # Remember: integers are also numeric

## [1] 5

custom_sqrt("17")                 # Error: not numeric

## Error in custom_sqrt("17"): Argument 'x' must be numeric!

custom_sqrt(vector("numeric", 0)) # Error: length is zero (not equal to 1)

## Error in custom_sqrt(vector("numeric", 0)): Argument 'x' must be of length 1!

custom_sqrt(c(1, 2, 3))           # Error: length > 1

## Error in custom_sqrt(c(1, 2, 3)): Argument 'x' must be of length 1!

custom_sqrt(-3)                   # Error: no positive numeric value

## Error in custom_sqrt(-3): Argument 'x' must be positive (>= 0)!

The sqrt() function implemented in base R does something similar, except that it also works for vectors with length \(> 1\) and only warns us if we apply it to negative values (returns NaN; see Missing values). However, when the input argument is a character we will get an error similar to our custom function.

sqrt(c(1, 2, 3))

## [1] 1.000000 1.414214 1.732051

sqrt(c(-3, -1, 1, 3))

## Warning in sqrt(c(-3, -1, 1, 3)): NaNs produced

## [1]      NaN      NaN 1.000000 1.732051

sqrt("foo")

## Error in sqrt("foo"): non-numeric argument to mathematical function

Short form

Instead of using three different checks in custom_sqrt() and three different error messages we could also combine everything in one single check using a logical | (or ||). Let us re-declare the function:

# Custom square root function
custom_sqrt <- function(x) {
    if (!is.numeric(x) || !length(x) == 1 || x < 0) stop("wrong input")
    return(sqrt(x))
}

Advantage: The function requires less typing and looks simpler.
Disadvantage: When an error is thrown, you will always get the same error message ("wrong input"), but you don’t really get any information what went wrong.

Some error messages are very easy to interpret and you immediately know what went wrong, while others look more sarcastic then helpful (see below). Having precise error messages can sometimes save hours of debugging and searching for the actual problem. Thus, rather write multiple separate checks than one large one with a super general error message.

An example out of the [Microsoft Windows documentation](https://docs.microsoft.com/en-us/windows/win32/uxguide/mess-error) on how error messages should not look like (but how we all know them).

Figure 7.2: An example out of the Microsoft Windows documentation on how error messages should not look like (but how we all know them).

Additional functions

There are few additional functions which might be of interest in combination with sanity checks. You will not need them to solve the exercises in this book, but these functions are very handy to simplify sanity checks.

Command	Description
`stopifnot()`	Throws an error if not evaluated to `TRUE`.
`inherits()`	Check of object contains a specific class.
`match.arg()`	Check if an input is allowed.
`file.exists()`	Check if a file exists.
`dir.exists()`	Check if a directory exists.

The examples below show some minimal examples how these commands work.

Stop if not: stopifnot() is a short version of if (!...) stop("error message") and throws an automatically generated error message if the logical expression evaluates to FALSE (stop if not TRUE; see ?stopifnot).

test_stopifnot <- function(x) {
    stopifnot(is.numeric(x))
    print(x)
}
test_stopifnot("character")

## Error in test_stopifnot("character"): is.numeric(x) is not TRUE

This could also be written as follows (with a custom error message).

test_stopifnot <- function(x) {
    if (!is.numeric(x)) stop("x must be numeric")
    return(x)
}
test_stopifnot("character")

## Error in test_stopifnot("character"): x must be numeric

Inherits: Argument x in the next function must either be a matrix or a character vector. inherits() checks if the return of class() of an object contains a specific class name.

test_inherits <- function(x) {
    stopifnot(inherits(x, c("matrix", "character")))
    return(x)
}
test_inherits(2L)

## Error in test_inherits(2L): inherits(x, c("matrix", "character")) is not TRUE

In this case, 2L is of class "integer" (check class(2L)) wherefore the test fails and an error is thrown. The same could be achieved differently, e.g.:

test_inherits <- function(x) {
    if (!is.matrix(x) & !is.character(x)) stop("x must be a matrix or a character vector")
    return(x)
}
test_inherits(2L)

## Error in test_inherits(2L): x must be a matrix or a character vector

Argument matching: Another smart way to only allow for special inputs is match.arg(). An argument can be defined with a series of allowed values. We can then check if the one provided by the user is actually among them.

test_matcharg <- function(x) {
    x <- match.arg(x, c("male", "female"))
    return(x)
}
test_matcharg("female")

## [1] "female"

test_matcharg("dog")

## Error in match.arg(x, c("male", "female")): 'arg' should be one of "male", "female"

Check if file exists: When you write a function which reads from a file or operates on a directory, file.exists() and dir.exists() can be used to check if the file/directory really exists.

test_fileexists <- function(file) {
    stopifnot(file.exists(file))
    return(file)
}
test_fileexists("my_dataset.rda")

## Error in test_fileexists("my_dataset.rda"): file.exists(file) is not TRUE

The same works for dir.exists() to check if a directory exists. Checking a directory and using if-conditions, this could look similar to the next function:

test_direxists <- function(dir) {
    if (!dir.exists(dir)) stop("Cannot find directory, does not exist.")
    return(dir)
}
test_direxists("Downloads")

## Error in test_direxists("Downloads"): Cannot find directory, does not exist.

Interested to learn more about boolean algebra? Or even participating in the course “198812 VU Computer Programming Prerequisites” by the DiSC? Feel free to have a look at this tutorial with boolean algebra exercises and how to do it in R. This is optional material and not part of the R programming course!