SS22 Scientific Coding with Julia

Not the most efficient way of computing $\pi$

As we very well know, there are a lot of ways to compute $\pi$ . There is even a blog entry in the Julia blog for that. Nevertheless, we decided for a different method (that is part of the introductory courses on JuliaAcademy).

A circle with radius $r$ has an area of

A_{circle} = \pi r^2

and the square that encases it

A_{square} = 4 r^2.

The ratio between the area of the circle and the area of the square is

\frac{A_{circle}}{A_{square}} = \frac{\pi r^2}{4 r^2} = \frac{\pi}{4}

and therefore we can define $\pi$ as

\pi = 4\frac{A_{circle}}{A_{square}}.

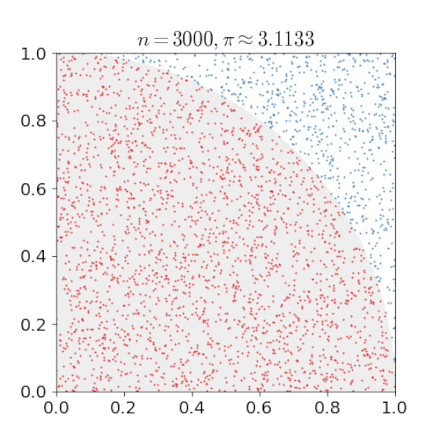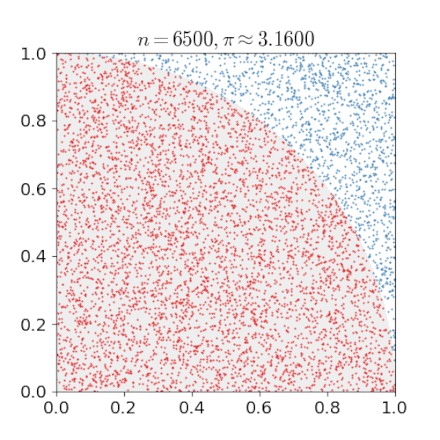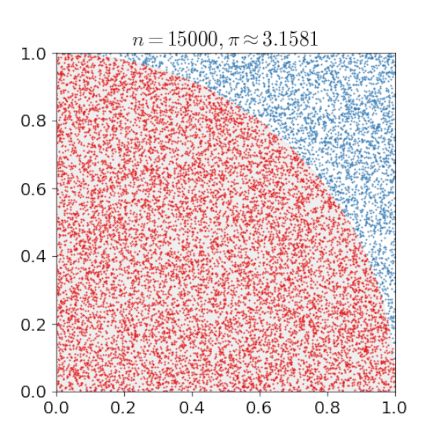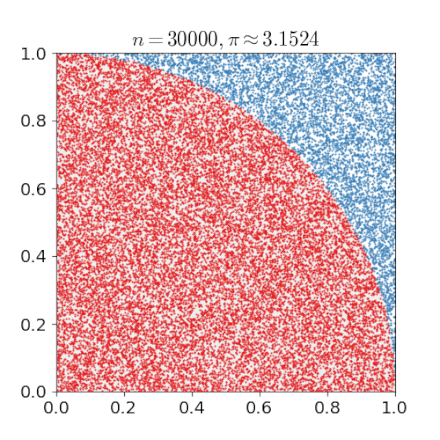
The same is true if we just take the first quadrant, so $\frac14$ of the square as well as the circle. This simplification will make the code more compact and faster.

The above formula suggests that we can compute $\pi$ by a Monte Carlo Method. Actually this example is also included in the Wiki article and it comes with this nice gif.

Simulation of the Monte Carlo Method for computing π. Original source:
https://commons.wikimedia.org/wiki/File:Pi_30K.gif

The algorithm therefore becomes:

For a given number $N$ of uniformly scattered points in the quadrant determine if these points are in the circle (distance less than 1) or not. We call the number of points in the circle $M$ .
Estimate $\pi$ by computing

\pi \approx 4 \frac{M}{N}.

Implement the above described algorithm to compute

\pi

Define a function that determines $M$ for a given integer $N$ .
Define a function that estimates $\pi$ for a given function $f$ and integer $N$ .
Test your code with different values for $N$ .

Help: The function rand() will give you a uniformly scattered point in the interval $[0,1]$ .

Solution

function in_unit_circle(N::Integer)
    M = 0
    
    for i in 1:N
        if (rand()^2 + rand()^2) < 1
            M += 1
        end
    end

    return M
end

function estimate_pi(f::Function, N::Integer)
    return 4 * f(N) / N
end

function get_accuracy(f::Function, N::Integer)
    return abs(
        estimate_pi(f, N) - pi
        )
end

N = 2^30
get_accuracy(in_unit_circle, N)

4.897092516031876e-5

CC BY-SA 4.0 - Gregor Ehrensperger, Peter Kandolf, Jonas Kusch. Last modified: September 09, 2022. Website built with Franklin.jl and the Julia programming language.

Not the most efficient way of computing π\piπ

Not the most efficient way of computing $\pi$