SS22 Scientific Coding with Julia

GPU computing in Julia

Introduction
Implicit parallelism programming
$\pi$ example on the GPU

Graphic Processing Units, or GPUs for short, were originally designed to manipulate images in a frame buffer. Their inherent parallelism makes them more efficient for some tasks than CPUs. Basically, everything that is related to SIMD operations but not limited to them. Using GPUs for general purpose computing (GPGPU) became a thing in the 21st century. NVIDIA was the first big vendor that started to support this kind of application for their GPUs and invested heavily in dedicated frameworks to aid general purpose computing and later also started to produce dedicated hardware for this purpose only. Nowadays, GPUs are used for artificial intelligence, deep learning and a lot of HPC workloads - some still use them for gaming too.

Introduction

In Julia, GPUs are supported by the JuliaGPU project. They support the three big vendor frameworks:

NVIDIA with CUDA and CUDA.jl
AMD with ROCm and AMDGPU.jl
Intel with oneAPI and oneAPI.jl
Apple with Apple's M1 GPUs Metal and Metal.jl (requires at least Julia 1.8)

where CUDA.jl comes with the most features. Nevertheless, in good Julia practice, the team behind JuliaGPU also included an abstraction layer, such that a lot of common functionality can be implemented without the need to specify a vendor and to do some generic GPU programming.

Compile strategy for JuliaGPU Original source:
https://www.youtube.com/watch?v=Hz9IMJuW5hU

Nevertheless, for the rest of the section, we will focus on CUDA.jl as the card at hand is CUDA compatible.

We install the package with Pkg.add("CUDA"); using CUDA and execute the test right away, to see if the GPU is working with Julia:

julia> using CUDA

(@v1.7) pkg> test CUDA
┌ Info: System information:
│ CUDA toolkit 11.7, artifact installation
│ NVIDIA driver 510.73.5, for CUDA 11.6
│ CUDA driver 11.6
│ 
│ Libraries: 
│ - CUBLAS: 11.10.1
│ - CURAND: 10.2.10
│ - CUFFT: 10.7.2
│ - CUSOLVER: 11.3.5
│ - CUSPARSE: 11.7.3
│ - CUPTI: 17.0.0
│ - NVML: 11.0.0+510.73.5
│ - CUDNN: 8.30.2 (for CUDA 11.5.0)
│ - CUTENSOR: 1.4.0 (for CUDA 11.5.0)
│ 
│ Toolchain:
│ - Julia: 1.7.3
│ - LLVM: 12.0.1
│ - PTX ISA support: 3.2, 4.0, 4.1, 4.2, 4.3, 5.0, 6.0, 6.1, 6.3, 6.4, 6.5, 7.0
│ - Device capability support: sm_35, sm_37, sm_50, sm_52, sm_53, sm_60, sm_61, sm_62, sm_70, sm_72, sm_75, sm_80
│ 
│ 1 device:
└   0: NVIDIA GeForce RTX 3070 Laptop GPU (sm_86, 7.787 GiB / 8.000 GiB available)
Test Summary: |  Pass  Broken  Total
  Overall     | 17002       5  17007
    SUCCESS
     Testing CUDA tests passed

The full output is in the example block to preserve a bit of readability.

(@v1.7) pkg> test CUDA
┌ Info: System information:
│ CUDA toolkit 11.7, artifact installation
│ NVIDIA driver 510.73.5, for CUDA 11.6
│ CUDA driver 11.6
│ 
│ Libraries: 
│ - CUBLAS: 11.10.1
│ - CURAND: 10.2.10
│ - CUFFT: 10.7.2
│ - CUSOLVER: 11.3.5
│ - CUSPARSE: 11.7.3
│ - CUPTI: 17.0.0
│ - NVML: 11.0.0+510.73.5
│ - CUDNN: 8.30.2 (for CUDA 11.5.0)
│ - CUTENSOR: 1.4.0 (for CUDA 11.5.0)
│ 
│ Toolchain:
│ - Julia: 1.7.3
│ - LLVM: 12.0.1
│ - PTX ISA support: 3.2, 4.0, 4.1, 4.2, 4.3, 5.0, 6.0, 6.1, 6.3, 6.4, 6.5, 7.0
│ - Device capability support: sm_35, sm_37, sm_50, sm_52, sm_53, sm_60, sm_61, sm_62, sm_70, sm_72, sm_75, sm_80
│ 
│ 1 device:
└   0: NVIDIA GeForce RTX 3070 Laptop GPU (sm_86, 7.787 GiB / 8.000 GiB available)
[ Info: Testing using 1 device(s): 0. NVIDIA GeForce RTX 3070 Laptop GPU (UUID bfdb6f60-dbcf-1a82-ca79-1c8b947c3f35)
                                                  |          | ---------------- GPU ---------------- | ---------------- CPU ---------------- |
Test                                     (Worker) | Time (s) | GC (s) | GC % | Alloc (MB) | RSS (MB) | GC (s) | GC % | Alloc (MB) | RSS (MB) |
Test                                     (Worker) | Time (s) | GC (s) | GC % | Alloc (MB) | RSS (MB) | GC (s) | GC % | Alloc (MB) | RSS (MB) |
initialization                                (2) |     5.64 |   0.00 |  0.0 |       0.00 |   165.00 |   0.08 |  1.4 |     512.27 |   843.59 |
gpuarrays/indexing scalar                     (2) |    25.43 |   0.00 |  0.0 |       0.01 |   181.00 |   1.20 |  4.7 |    4688.43 |   843.59 |
gpuarrays/reductions/reducedim!               (2) |    90.88 |   0.00 |  0.0 |       1.03 |   183.00 |   8.52 |  9.4 |   22482.18 |  1163.61 |
gpuarrays/linalg                              (2) |    54.46 |   0.00 |  0.0 |      11.59 |   551.00 |   3.43 |  6.3 |   10524.64 |  2332.89 |
gpuarrays/math/power                          (2) |    35.13 |   0.00 |  0.0 |       0.01 |   551.00 |   3.23 |  9.2 |    8032.86 |  2492.46 |
gpuarrays/linalg/mul!/vector-matrix           (2) |    55.05 |   0.00 |  0.0 |       0.02 |   551.00 |   3.45 |  6.3 |   11596.70 |  2833.54 |
gpuarrays/indexing multidimensional           (2) |    37.84 |   0.00 |  0.0 |       1.21 |   183.00 |   2.40 |  6.4 |    7920.18 |  2833.54 |
gpuarrays/interface                           (2) |     4.45 |   0.00 |  0.0 |       0.00 |   181.00 |   0.31 |  6.9 |     858.64 |  2833.54 |
gpuarrays/reductions/any all count            (2) |    16.45 |   0.00 |  0.0 |       0.00 |   181.00 |   1.46 |  8.9 |    4293.68 |  2833.54 |
gpuarrays/reductions/minimum maximum extrema  (2) |   140.12 |   0.01 |  0.0 |       1.41 |   185.00 |  10.18 |  7.3 |   31924.33 |  2954.52 |
gpuarrays/uniformscaling                      (2) |     8.35 |   0.00 |  0.0 |       0.01 |   181.00 |   0.41 |  4.9 |    1288.85 |  2954.52 |
gpuarrays/linalg/mul!/matrix-matrix           (2) |   107.47 |   0.01 |  0.0 |       0.12 |   553.00 |   6.31 |  5.9 |   19136.07 |  4212.98 |
gpuarrays/math/intrinsics                     (2) |     3.74 |   0.00 |  0.0 |       0.00 |   181.00 |   0.19 |  5.0 |     711.11 |  4212.98 |
gpuarrays/linalg/norm                         (2) |   268.94 |   0.01 |  0.0 |       0.02 |   257.00 |  21.18 |  7.9 |   52430.53 |  5626.27 |
gpuarrays/statistics                          (2) |    77.79 |   0.00 |  0.0 |       1.51 |   551.00 |   4.21 |  5.4 |   13876.69 |  6655.55 |
gpuarrays/reductions/mapreduce                (2) |   203.11 |   0.01 |  0.0 |       1.81 |   185.00 |  11.73 |  5.8 |   37609.42 |  6729.29 |
gpuarrays/constructors                        (2) |    19.20 |   0.00 |  0.0 |       0.08 |   181.00 |   0.68 |  3.5 |    2569.40 |  6729.29 |
gpuarrays/random                              (2) |    28.17 |   0.00 |  0.0 |       0.03 |   181.00 |   1.52 |  5.4 |    4786.98 |  6729.29 |
gpuarrays/base                                (2) |    26.12 |   0.00 |  0.0 |       8.82 |   181.00 |   1.37 |  5.2 |    4506.52 |  6816.72 |
gpuarrays/reductions/== isequal               (2) |    98.03 |   0.01 |  0.0 |       1.07 |   183.00 |  10.38 | 10.6 |   16597.95 |  7809.12 |
gpuarrays/broadcasting                        (2) |   362.62 |   0.01 |  0.0 |       2.00 |   185.00 |  42.96 | 11.8 |   53772.92 |  8699.58 |
gpuarrays/reductions/mapreducedim!            (2) |    56.83 |   0.00 |  0.0 |       1.54 |   183.00 |   6.86 | 12.1 |    7394.71 |  8699.58 |
gpuarrays/reductions/reduce                   (2) |    19.58 |   0.00 |  0.0 |       1.21 |   183.00 |   0.44 |  2.3 |    2226.51 |  8699.58 |
gpuarrays/reductions/sum prod                 (2) |   279.16 |   0.01 |  0.0 |       3.24 |   185.00 |  34.08 | 12.2 |   40919.47 | 10091.04 |
apiutils                                      (2) |     0.11 |   0.00 |  0.0 |       0.00 |   165.00 |   0.00 |  0.0 |       0.81 | 10091.04 |
array                                         (2) |   153.18 |   0.01 |  0.0 |    1266.37 |  1341.00 |  36.18 | 23.6 |   19461.83 | 10680.45 |
broadcast                                     (2) |    22.37 |   0.00 |  0.0 |       0.00 |  1333.00 |   3.60 | 16.1 |    2901.68 | 10680.45 |
codegen                                       (2) |    10.09 |   0.00 |  0.0 |       0.00 |  1393.00 |   1.39 | 13.7 |    1456.06 | 10680.45 |
cublas                                        (2) |    83.06 |   0.02 |  0.0 |      14.55 |  1717.00 |   9.41 | 11.3 |   12030.98 | 11289.79 |
cudadrv                                       (2) |     6.99 |   0.00 |  0.0 |       0.00 |  1335.00 |   0.28 |  4.1 |     791.80 | 11308.88 |
cufft                                         (2) |    24.73 |   0.00 |  0.0 |     233.38 |  1437.00 |   2.91 | 11.8 |    2843.60 | 11314.30 |
curand                                        (2) |     0.17 |   0.00 |  0.0 |       0.00 |  1327.00 |   0.09 | 50.0 |       3.75 | 11314.30 |
cusparse                                      (2) |    49.55 |   0.02 |  0.0 |      10.81 |  1491.00 |   2.72 |  5.5 |    5858.52 | 11459.28 |
examples                                      (2) |    85.06 |   0.00 |  0.0 |       0.00 |  1317.00 |   0.00 |  0.0 |      45.06 | 11459.28 |
exceptions                                    (2) |    53.14 |   0.00 |  0.0 |       0.00 |  1317.00 |   0.00 |  0.0 |       1.57 | 11459.28 |
execution                                        (2) |    94.27 |   0.00 |  0.0 |       0.49 |  1401.00 |  21.67 | 23.0 |   11410.60 | 11459.28 |
iterator                                      (2) |     2.11 |   0.00 |  0.0 |       1.93 |  1317.00 |   0.00 |  0.0 |     360.93 | 11459.28 |
linalg                                        (2) |    38.90 |   0.00 |  0.0 |       9.03 |  1405.00 |   8.86 | 22.8 |    5066.35 | 11459.28 |
nvml                                          (2) |     0.51 |   0.00 |  0.0 |       0.00 |  1317.00 |   0.00 |  0.0 |      28.69 | 11459.28 |
nvtx                                          (2) |     0.23 |   0.00 |  0.0 |       0.00 |  1317.00 |   0.00 |  0.0 |      34.94 | 11459.28 |
pointer                                       (2) |     0.25 |   0.00 |  0.0 |       0.00 |  1317.00 |   0.00 |  0.0 |      11.54 | 11459.28 |
pool                                          (2) |     4.44 |   0.00 |  0.0 |       0.00 |   165.00 |   2.79 | 62.9 |     244.88 | 11459.28 |
random                                        (2) |    31.17 |   0.00 |  0.0 |     256.58 |   445.00 |   6.35 | 20.4 |    3519.72 | 11459.28 |
sorting                                       (2) |   227.27 |   0.01 |  0.0 |     543.84 |  1777.00 |  50.72 | 22.3 |   28578.54 | 13741.85 |
texture                                       (2) |    54.81 |   0.00 |  0.0 |       0.09 |   443.00 |   8.27 | 15.1 |    7309.86 | 13741.85 |
threading                                     (2) |     2.94 |   0.00 |  0.0 |      10.94 |   811.00 |   0.45 | 15.5 |     299.54 | 13741.85 |
utils                                         (2) |     0.80 |   0.00 |  0.0 |       0.00 |   421.00 |   0.00 |  0.0 |      76.69 | 13741.85 |
cudnn/activation                              (2) |     1.83 |   0.00 |  0.0 |       0.00 |   545.00 |   0.14 |  7.4 |     186.83 | 13741.85 |
cudnn/convolution                             (2) |     0.07 |   0.00 |  0.0 |       0.00 |   421.00 |   0.00 |  0.0 |       6.14 | 13741.85 |
cudnn/dropout                                 (2) |     1.37 |   0.00 |  0.0 |       1.43 |   549.00 |   0.22 | 16.1 |      88.64 | 13741.85 |
cudnn/inplace                                 (2) |     0.85 |   0.00 |  0.0 |       0.01 |   549.00 |   0.19 | 22.4 |      50.14 | 13741.85 |
cudnn/multiheadattn                           (2) |    12.14 |   0.00 |  0.0 |       0.15 |   927.00 |   1.91 | 15.7 |    1592.27 | 13741.85 |
cudnn/normalization                           (2) |    15.76 |   0.00 |  0.0 |       0.08 |   589.00 |   1.66 | 10.6 |    1682.89 | 13766.65 |
cudnn/optensor                                (2) |     1.24 |   0.00 |  0.0 |       0.00 |   545.00 |   0.13 | 10.7 |     136.46 | 13766.79 |
cudnn/pooling                                 (2) |     4.49 |   0.00 |  0.0 |       0.06 |   545.00 |   0.17 |  3.8 |     666.79 | 13766.79 |
cudnn/reduce                                  (2) |     1.42 |   0.00 |  0.0 |       0.02 |   545.00 |   0.14 | 10.0 |     207.65 | 13766.79 |
cudnn/rnn                                     (2) |     6.24 |   0.00 |  0.1 |     898.13 |  1567.00 |   0.22 |  3.4 |     649.49 | 13865.52 |
cudnn/softmax                                 (2) |     0.98 |   0.00 |  0.0 |       0.01 |  1185.00 |   0.12 | 12.5 |      73.36 | 13865.70 |
cudnn/tensor                                  (2) |     1.99 |   0.00 |  0.0 |       0.00 |   175.00 |   1.65 | 83.0 |      25.64 | 13865.70 |
cusolver/dense                                (2) |   136.80 |   0.04 |  0.0 |    1467.10 |   617.00 |  29.02 | 21.2 |   15502.48 | 14179.64 |
cusolver/multigpu                             (2) |     7.68 |   0.00 |  0.0 |     545.89 |   979.00 |   0.19 |  2.5 |     991.26 | 14179.64 |
cusolver/sparse                               (2) |     5.29 |   0.00 |  0.0 |       0.18 |   721.00 |   0.37 |  6.9 |     420.74 | 14179.64 |
cusparse/broadcast                            (2) |    75.65 |   0.00 |  0.0 |       0.02 |   617.00 |  14.20 | 18.8 |    8232.49 | 14371.40 |
cusparse/conversions                          (2) |     8.84 |   0.00 |  0.0 |       0.02 |   615.00 |   0.50 |  5.7 |    1089.83 | 14371.40 |
cusparse/device                               (2) |     0.32 |   0.00 |  0.0 |       0.01 |   615.00 |   0.11 | 34.3 |       3.66 | 14371.40 |
cusparse/generic                              (2) |     1.85 |   0.00 |  0.0 |       0.05 |   615.00 |   0.11 |  5.9 |     182.92 | 14371.40 |
cusparse/interfaces                           (2) |    34.24 |   0.01 |  0.0 |       0.97 |   615.00 |   3.63 | 10.6 |    3770.70 | 14371.40 |
cusparse/linalg                               (2) |     4.44 |   0.00 |  0.0 |       0.01 |   615.00 |   0.10 |  2.2 |     560.27 | 14371.40 |
cutensor/base                                 (2) |     0.11 |   0.00 |  0.0 |       0.05 |   517.00 |   0.00 |  0.0 |      14.68 | 14371.40 |
cutensor/contractions                         (2) |    22.99 |   0.01 |  0.0 |   10626.41 |  1911.00 |   1.12 |  4.9 |    3072.22 | 14597.90 |
cutensor/elementwise_binary                   (2) |    21.48 |   0.00 |  0.0 |       6.11 |  1427.00 |   0.78 |  3.6 |    2347.49 | 14597.90 |
cutensor/elementwise_trinary                  (2) |    26.38 |   0.00 |  0.0 |       2.71 |  1427.00 |   0.98 |  3.7 |    3145.61 | 14597.90 |
cutensor/permutations                         (2) |     2.94 |   0.00 |  0.0 |       1.36 |  1427.00 |   0.12 |  3.9 |     312.68 | 14597.90 |
cutensor/reductions                           (2) |    22.97 |   0.00 |  0.0 |      36.36 |  1427.00 |   0.42 |  1.8 |    2181.72 | 15127.08 |
device/array                                  (2) |     8.47 |   0.00 |  0.0 |       0.00 |  1333.00 |   0.33 |  3.9 |    1149.69 | 15127.08 |
device/intrinsics                             (2) |    56.15 |   0.00 |  0.0 |       0.00 |  2015.00 |  10.61 | 18.9 |    7190.85 | 15161.48 |
device/ldg                                    (2) |    10.23 |   0.00 |  0.0 |       0.00 |  1333.00 |   0.33 |  3.3 |    1598.80 | 15161.48 |
device/random                                 (2) |    70.45 |   0.00 |  0.0 |       0.17 |  1335.00 |  13.64 | 19.4 |    7687.06 | 15161.48 |
device/intrinsics/atomics                     (2) |   122.21 |   0.00 |  0.0 |       0.00 |  1335.00 |  24.14 | 19.7 |   13241.89 | 15169.65 |
device/intrinsics/math                        (2) |    87.89 |   0.00 |  0.0 |       0.00 |  1363.00 |  15.47 | 17.6 |    8747.68 | 15202.04 |
device/intrinsics/memory                      (2) |    33.16 |   0.00 |  0.0 |       0.02 |  1333.00 |   6.44 | 19.4 |    4266.41 | 15202.04 |
device/intrinsics/output                      (2) |    38.30 |   0.00 |  0.0 |       0.00 |  1333.00 |   8.02 | 20.9 |    4777.54 | 15202.04 |
device/intrinsics/wmma                        (2) |   132.81 |   0.01 |  0.0 |       0.63 |  1337.00 |  28.43 | 21.4 |   15981.42 | 15469.16 |
Testing finished in 1 hour, 10 minutes, 21 seconds, 161 milliseconds

Test Summary: |  Pass  Broken  Total
  Overall     | 17002       5  17007
    SUCCESS
     Testing CUDA tests passed

The output of the test already provides us with a lot of information about the card and the supported CUDA library versions. Note that CUDA.jl will look up the NVIDIA driver (the only requirement) and download the best CUDA version on its own. Therefore, it is not necessarily the same version as installed on the system.

Right away, we are able to use the high level functionality of the CUDA.jl package with the implicit parallelism programming model.

Implicit parallelism programming

Let us look at some examples:

julia> a = CuArray([1.0, 2.0, 3.0, 4.0])
4-element CuArray{Float64, 1, CUDA.Mem.DeviceBuffer}:
 1.0
 2.0
 3.0
 4.0

julia> a .+= 1
4-element CuArray{Float64, 1, CUDA.Mem.DeviceBuffer}:
 2.0
 3.0
 4.0
 5.0

julia> a .+= a
4-element CuArray{Float64, 1, CUDA.Mem.DeviceBuffer}:
  4.0
  6.0
  8.0
 10.0

julia> sum(a)
28.0

julia> A = a * a'
4×4 CuArray{Float64, 2, CUDA.Mem.DeviceBuffer}:
 16.0  24.0  32.0   40.0
 24.0  36.0  48.0   60.0
 32.0  48.0  64.0   80.0
 40.0  60.0  80.0  100.0

julia> d = CUDA.rand(length(a))
4-element CuArray{Float32, 1, CUDA.Mem.DeviceBuffer}:
 0.2327924
 0.06764824
 0.7085522
 0.97067034

julia> using LinearAlgebra

julia> mul!(d, A, d)
ERROR: ArgumentError: output matrix must not be aliased with input matrix
Stacktrace:
 [1] gemm_dispatch!(C::CuArray{Float32, 1, CUDA.Mem.DeviceBuffer}, A::CuArray{Float64, 2, CUDA.Mem.DeviceBuffer}, B::CuArray{Float32, 1, CUDA.Mem.DeviceBuffer}, alpha::Bool, beta::Bool)
   @ CUDA.CUBLAS ~/.julia/packages/CUDA/tTK8Y/lib/cublas/linalg.jl:269
 [2] gemv_dispatch!(Y::CuArray{Float32, 1, CUDA.Mem.DeviceBuffer}, A::CuArray{Float64, 2, CUDA.Mem.DeviceBuffer}, B::CuArray{Float32, 1, CUDA.Mem.DeviceBuffer}, alpha::Bool, beta::Bool)
   @ CUDA.CUBLAS ~/.julia/packages/CUDA/tTK8Y/lib/cublas/linalg.jl:181
 [3] mul!
   @ ~/.julia/packages/CUDA/tTK8Y/lib/cublas/linalg.jl:188 [inlined]
 [4] mul!(C::CuArray{Float32, 1, CUDA.Mem.DeviceBuffer}, A::CuArray{Float64, 2, CUDA.Mem.DeviceBuffer}, B::CuArray{Float32, 1, CUDA.Mem.DeviceBuffer})
   @ LinearAlgebra /opt/julia-1.7.3/share/julia/stdlib/v1.7/LinearAlgebra/src/matmul.jl:275
 [5] top-level scope
   @ REPL[23]:1
 [6] top-level scope
   @ ~/.julia/packages/CUDA/tTK8Y/src/initialization.jl:52

julia> d = CUDA.rand(Float64, length(a))
4-element CuArray{Float64, 1, CUDA.Mem.DeviceBuffer}:
 0.6985405365128223
 0.1389900111808831
 0.41880569903314474
 0.47366941788943956

julia> mul!(d, A, d)
4-element CuArray{Float64, 1, CUDA.Mem.DeviceBuffer}:
  46.86096793718457
  70.29145190577685
  93.72193587436914
 117.15241984296142

julia> qr(d)
CUDA.CUSOLVER.CuQR{Float64, CuArray{Float64, 2, CUDA.Mem.DeviceBuffer}} with factors Q and R:
[┌ Warning: Performing scalar indexing on task Task (runnable) @0x00007f27b8a15150.
│ Invocation of CuQRPackedQ getindex resulted in scalar indexing of a GPU array.
│ This is typically caused by calling an iterating implementation of a method.
│ Such implementations *do not* execute on the GPU, but very slowly on the CPU,
│ and therefore are only permitted from the REPL for prototyping purposes.
│ If you did intend to index this array, annotate the caller with @allowscalar.
└ @ GPUArraysCore ~/.julia/packages/GPUArraysCore/rSIl2/src/GPUArraysCore.jl:81
-0.2721655269759087 -0.40824829046386296 -0.5443310539518174 -0.6804138174397716; -0.40824829046386296 0.8689897948556636 -0.17468027352578192 -0.21835034190722735; -0.5443310539518174 -0.1746802735257819 0.7670929686322908 -0.29113378920963645; -0.6804138174397716 -0.21835034190722735 -0.2911337892096365 0.6360827634879545]
[-172.17819044853752;;]

julia> broadcast(a) do x sin(x) end
4-element CuArray{Float64, 1, CUDA.Mem.DeviceBuffer}:
 -0.7568024953079282
 -0.27941549819892586
  0.9893582466233818
 -0.5440211108893699

julia> reduce(+, a)
28.0

julia> accumulate(+, a)
4-element CuArray{Float64, 1, CUDA.Mem.DeviceBuffer}:
  4.0
 10.0
 18.0
 28.0

With this functionality we can code up a lot of problems in scientific computing and port it to the GPU without knowing anything else than how to include CUDA.jl and define/allocate the appropriate data on the GPU. It is worth noting, that this is also highly efficient, as the people behind CUDA.jl optimize the calls with the same features as Julia itself and they work extraordinary well.

Of course we can not express everything in these terms. Sometimes it is necessary to write a specific CUDA kernel function. Note, that kernel is the technical name given to a function that is executed on the GPU.

$\pi$ example on the GPU

The main idea is to use the most of the GPU by performing as many operations in parallel as possible, this also means we need to represent M as a vector again. The GPU at hand supports a maximum of 1024 threads, so let us use all of them.

There is also one additional thing to keep in mind, that is, a kernel can not return a value. That means we need to give M as an input variable rather than an output variable and in order to stick to the Julia convention we define the kernel as:

function in_unit_circle_kernel!(n::Int64, M)
    j =  threadIdx().x 
    
    for i in 1:n
        if (rand()^2 + rand()^2) < 1
            @inbounds M[j] += 1
        end
    end

    return nothing
end

This looks very similar to our function in_unit_circle_threaded3. Instead of threadid() as we had it in multithreading, this time the id is queried by threadIdx().x. The .x is due to the fact that we could also have two or three dimensional arrays (remember GPUs were designed to work with images).

The kernel is now called with the @cuda macro and the number of threads given as an argument. Note, that we also define M to have dimension $2^{10} = 1024$ and of type Int8.

We use Int8 as on GPUs the data type has quite a high impact on the performance. With integers this is not that important but if we are not working on a high level server grades GPU the double (Float64) performance will be significantly slower than single (Float32). Secondly, there is usually less storage on the GPU.

The resulting host side function looks as follows:

function in_unit_circle_gpu(N::Int64)
    nthreads = 2^10
    len, _ = divrem(N, nthreads)
    M = CUDA.zeros(Int8, nthreads)

    @cuda threads = nthreads in_unit_circle_kernel!(len, M)

    return sum(M)
end

and the performance:

julia> get_accuracy(in_unit_circle_gpu, N)
  6.65503269949852e-5

julia> @btime estimate_pi(in_unit_circle_gpu, N);
  1.740 s (157 allocations: 8.25 KiB)

We are already faster than the standard Julia implementation but this is not what we were hoping for. The used GPU is actually quite powerful and if we have a look at the NVIDIA System Management Interface (nvidia-smi) on the terminal we see that GPU is not utilized fully.

+-----------------------------------------------------------------------------+
| NVIDIA-SMI 510.73.05    Driver Version: 510.73.05    CUDA Version: 11.6     |
|-------------------------------+----------------------+----------------------+
| GPU  Name        Persistence-M| Bus-Id        Disp.A | Volatile Uncorr. ECC |
| Fan  Temp  Perf  Pwr:Usage/Cap|         Memory-Usage | GPU-Util  Compute M. |
|                               |                      |               MIG M. |
|===============================+======================+======================|
|   0  NVIDIA GeForce ...  Off  | 00000000:01:00.0 Off |                  N/A |
| N/A   38C    P5    15W /  N/A |    173MiB /  8192MiB |      0%      Default |
|                               |                      |                  N/A |
+-------------------------------+----------------------+----------------------+
                                                                               
+-----------------------------------------------------------------------------+
| Processes:                                                                  |
|  GPU   GI   CI        PID   Type   Process name                  GPU Memory |
|        ID   ID                                                   Usage      |
|=============================================================================|
|    0   N/A  N/A      2232      G   /usr/lib/xorg/Xorg                  4MiB |
|    0   N/A  N/A     46980      C   julia                             165MiB |
+-----------------------------------------------------------------------------+

It only provides a snapshot but we still see that the Volatile GPU-Util is low to insignificant. What we did in the above example was to use the maximal number of threads (1024) support by the used GPU and performed our operations with them. This way we only occupied one streaming multiprocessor (SM) but the GPU has several SMs - this is similar to how a CPU has multiple cores.

Multiple Streaming Multiprocessors

To get the full performance, we need to run our kernel not just with multiple threads, but also with multiple blocks.

In this technical blog from NVIDIA CUDA Refresher: The CUDA Programming Model we can read more about it. The following figure illustrates it quite nicely:

Kernel execution on GPU. Original source:
https://developer.nvidia.com/blog/cuda-refresher-cuda-programming-model/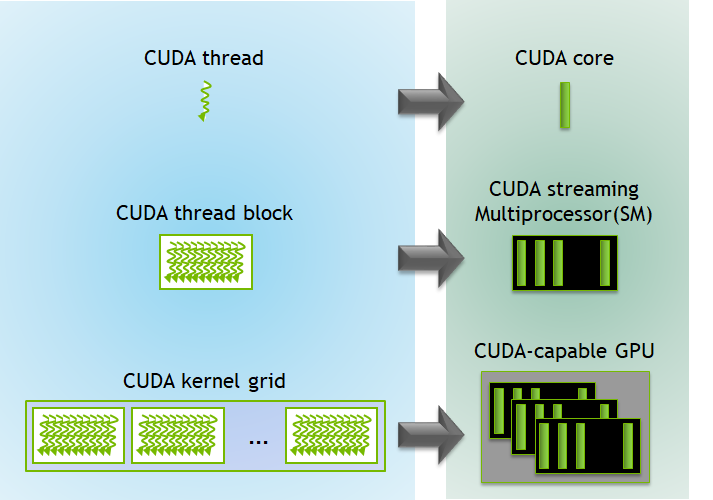

If we use blocks, the computation of our index in M becomes a bit more tricky to compute and we also need to have more storage for M.

Similar as with the threadIdx().x we have a blockIdx().x and a blockDim().x to perform this computation.

Julia starts with indexing by 1. On the GPU this can become a bit confusing as CUDA in general does not. In this case we need to correct the blockIdx() by 1.

As highlighted in the blog, CUDA.jl introduced optimized index types for CUDA to make sure that no storage is wasted. Therefore, we use 0x1 instead of 1 in the kernels in this section, where needed.

So we end up with the following code:

function in_unit_circle_kernel2!(M)
    j = (blockIdx().x - 0x1) * blockDim().x + threadIdx().x

    if (rand()^2 + rand()^2) < 1
        @inbounds M[j] += 1
    end

    return nothing
end

function in_unit_circle_gpu2(N::Int64)
    nthreads = 2^10
    nblocks, _ = divrem(N, nthreads)
    M = CUDA.zeros(Int8, N)

    @cuda threads = nthreads blocks = nblocks in_unit_circle_kernel2!(M)

    return sum(M)
end

and the performance:

julia> get_accuracy(in_unit_circle_gpu2, N)
  1.79504328450264e-5

julia> @btime estimate_pi(in_unit_circle_gpu2, N);
  81.436 ms (156 allocations: 8.16 KiB)

Now each thread on the GPU is doing exactly one computation (and therefore the loop inside the kernel is not needed and for performance reasons removed). This is still not the most efficient way to use the GPU and in addition it is rather wasteful on memory.

Multiple operations per thread

So let us optimize the computation a bit further. Each of the threads should do n iterations. This means we need to define the number of blocks as

n_{\operatorname{blocks}} = \frac{N}{n_{\operatorname{threads}} n}.

The kernel is a combination of the two previous kernels:

function in_unit_circle_kernel3!(n::Int64, M)
    j = (blockIdx().x - 0x1) * blockDim().x + threadIdx().x

    for _ in 1:n
        if (rand()^2 + rand()^2) < 1
            @inbounds M[j] += 1
        end
    end

    return nothing
end

The calling function needs to compute the values as defined above:

function in_unit_circle_gpu3(N::Int64)
    nthreads = 2^10
    n = 2^6
    
    nblocks, _ = divrem(N, n * nthreads)
    M = CUDA.zeros(Int8, nblocks * nthreads)
    
    @cuda threads = nthreads blocks = nblocks in_unit_circle_kernel3!(n, M)

    return sum(M)
end

and the performance is pretty good

julia> get_accuracy(in_unit_circle_gpu2, N)
  5.6093680210977936e-5

julia> @btime estimate_pi(in_unit_circle_gpu2, N);
  45.194 ms (155 allocations: 8.14 KiB)

One thing we have to keep in mind, is that we have defined M of type Int8 to save space and boost performance. If n become larger than $2^7$ it might happen that the result is too large and can no longer be stored in an 8-Bit integer (as a result an overflow would occur).

Additional notes

Like with the rest of the topics in this section we skimmed the surface and did not make a deep dive (like memory access, profiling to find slow parts in the code, multi GPU programming, multithreaded/distributed computing with GPUs and so forth). Have a look at the excellent introduction on JuliaGPU to see more about the topic and have a look at the YouTube Videos of Tim Besard for a start. Here it was only possible to give a sound idea on what is happening and how great and easy we can achieve all of it with Julia.

CC BY-SA 4.0 - Gregor Ehrensperger, Peter Kandolf, Jonas Kusch. Last modified: September 09, 2022. Website built with Franklin.jl and the Julia programming language.